BSP 房间地牢

关于本教程

本教程是免费且开源的，所有代码均使用 MIT 许可证 - 因此您可以随意使用。我希望您喜欢本教程，并制作出伟大的游戏！

如果您喜欢这个教程并希望我继续写作，请考虑支持我的 Patreon。

一种流行的地图生成方法是使用“二叉空间分割”（binary space partition, BSP）将您的地图细分为大小不一的矩形，然后将生成的房间连接成走廊。你可以用这种方法走很远的路：Nethack 广泛使用它，Dungeon Crawl: Stone Soup 有时使用它，而我的项目 - One Knight in the Dungeon - 在下水道关卡中使用它。本章将使用上一章的可视化工具来引导您使用这项技术。

实现一个新的地图 - 细分 BSP，样板代码

我们将从在 map_builders 中创建一个新文件开始 - bsp_dungeon.rs。我们首先创建基本的 BspDungeonBuilder 结构体：

#![allow(unused)]
fn main() {
pub struct BspDungeonBuilder {
    map : Map,
    starting_position : Position,
    depth: i32,
    rooms: Vec<Rect>,
    history: Vec<Map>,
    rects: Vec<Rect>
}
}

这基本上与 SimpleMapBuilder 中的结构体相同 - 并且我们保留了 rooms 向量，因为此方法也使用了房间的概念。我们添加了一个 rects 向量：该算法大量使用它，因此在整个实现过程中使其可用很有帮助。我们很快就会明白为什么需要它。

现在我们为该类型实现 MapBuilder 特征：

#![allow(unused)]
fn main() {
impl MapBuilder for BspDungeonBuilder {
    fn get_map(&self) -> Map {
        self.map.clone()
    }

    fn get_starting_position(&self) -> Position {
        self.starting_position.clone()
    }

    fn get_snapshot_history(&self) -> Vec<Map> {
        self.history.clone()
    }

    fn build_map(&mut self)  {
        // 我们应该在这里做一些事情
    }

    fn spawn_entities(&mut self, ecs : &mut World) {
        for room in self.rooms.iter().skip(1) {
            spawner::spawn_room(ecs, room, self.depth);
        }
    }

    fn take_snapshot(&mut self) {
        if SHOW_MAPGEN_VISUALIZER {
            let mut snapshot = self.map.clone();
            for v in snapshot.revealed_tiles.iter_mut() {
                *v = true;
            }
            self.history.push(snapshot);
        }
    }
}
}

这也几乎与 SimpleMapBuilder 相同，但 build_map 有一条注释提醒我们编写一些代码。如果您现在运行生成器，您将得到一个实心的墙块 - 并且没有任何内容。

我们还需要为 BspMapBuilder 实现一个 构造器。同样，它基本上与 SimpleMapBuilder 相同：

#![allow(unused)]
fn main() {
impl BspDungeonBuilder {
    pub fn new(new_depth : i32) -> BspDungeonBuilder {
        BspDungeonBuilder{
            map : Map::new(new_depth),
            starting_position : Position{ x: 0, y : 0 },
            depth : new_depth,
            rooms: Vec::new(),
            history: Vec::new(),
            rects: Vec::new()
        }
    }
}
}

最后，我们将打开 map_builders/mod.rs 并更改 random_builder 函数，使其始终返回我们的新地图类型：

#![allow(unused)]
fn main() {
pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> {
    // 请注意，在我们有第二种地图类型之前，这甚至不是轻微的随机
    Box::new(BspDungeonBuilder::new(new_depth))
}
}

再次说明，这根本不是随机的 - 但开发一个始终运行的功能要容易得多，而不是不断尝试直到它选择了我们想要调试的功能！

构建地图创建器

我们稍后会担心更换地图类型。现在开始制作地图！请注意，此实现是从我的 C++ 游戏 One Knight in the Dungeon 移植过来的。我们将从房间生成开始。在我们的 impl BspMapBuilder 中，我们添加一个新函数：

#![allow(unused)]
fn main() {
fn build(&mut self) {
    let mut rng = RandomNumberGenerator::new();

    self.rects.clear();
    self.rects.push( Rect::new(2, 2, self.map.width-5, self.map.height-5) ); // 从一个单一的地图大小的矩形开始
    let first_room = self.rects[0];
    self.add_subrects(first_room); // 划分第一个房间

    // 最多 240 次，我们获取一个随机矩形并划分它。 如果有可能在那里挤出一个
    // 房间，我们放置它并将其添加到房间列表。
    let mut n_rooms = 0;
    while n_rooms < 240 {
        let rect = self.get_random_rect(&mut rng);
        let candidate = self.get_random_sub_rect(rect, &mut rng);

        if self.is_possible(candidate) {
            apply_room_to_map(&mut self.map, &candidate);
            self.rooms.push(candidate);
            self.add_subrects(rect);
            self.take_snapshot();
        }

        n_rooms += 1;
    }
    let start = self.rooms[0].center();
    self.starting_position = Position{ x: start.0, y: start.1 };
}
}

那么这到底做了什么？

我们清除了作为构建器一部分创建的 rects 结构。这将用于存储从整个地图派生的矩形。
我们创建了“第一个房间” - 这实际上是整个地图。我们修剪了一点，为地图的侧面添加了一些填充。
我们调用 add_subrects，将矩形列表和第一个房间传递给它。我们将在稍后实现它，但它的作用是：它将矩形划分为四个象限，并将每个象限添加到矩形列表。
现在我们设置一个房间计数器，这样我们就不会无限循环。
当该计数器小于 240 时（一个相对任意的限制，可以产生有趣的结果）：
1. 我们调用 get_random_rect 以从矩形列表中检索一个随机矩形。
2. 我们使用此矩形作为外部边界调用 get_random_sub_rect。它在父矩形内的某个位置创建一个大小为 3 到 10 个图块（在每个轴上）的随机房间。
3. 我们询问 is_possible 候选房间是否可以绘制到地图上；每个图块都必须在地图边界内，并且还不是房间。如果是可能的：
  1. 我们在地图上标记它。
  2. 我们将其添加到房间列表。
  3. 我们调用 add_subrects 来细分我们刚刚使用的矩形（不是候选房间！）。

这里有很多支持函数在起作用，所以让我们逐一介绍它们。

#![allow(unused)]
fn main() {
fn add_subrects(&mut self, rect : Rect) {
    let width = i32::abs(rect.x1 - rect.x2);
    let height = i32::abs(rect.y1 - rect.y2);
    let half_width = i32::max(width / 2, 1);
    let half_height = i32::max(height / 2, 1);

    self.rects.push(Rect::new( rect.x1, rect.y1, half_width, half_height ));
    self.rects.push(Rect::new( rect.x1, rect.y1 + half_height, half_width, half_height ));
    self.rects.push(Rect::new( rect.x1 + half_width, rect.y1, half_width, half_height ));
    self.rects.push(Rect::new( rect.x1 + half_width, rect.y1 + half_height, half_width, half_height ));
}
}

函数 add_subrects 是 BSP（二叉空间分割）方法的关键：它接受一个矩形，并将宽度和高度平分。然后它创建四个新的矩形，每个象限对应一个。这些被添加到 rects 列表中。图形化表示：

###############        ###############
#             #        #  1   +   2  #
#             #        #      +      #
#      0      #   ->   #+++++++++++++#
#             #        #   3  +   4  #
#             #        #      +      #
###############        ###############

接下来是 get_random_rect：

#![allow(unused)]
fn main() {
fn get_random_rect(&mut self, rng : &mut RandomNumberGenerator) -> Rect {
    if self.rects.len() == 1 { return self.rects[0]; }
    let idx = (rng.roll_dice(1, self.rects.len() as i32)-1) as usize;
    self.rects[idx]
}
}

这是一个简单的函数。如果 rects 列表中只有一个矩形，它将返回第一个矩形。否则，它会掷一个骰子 1d(rects 列表的大小)，并返回在随机索引处找到的矩形。

接下来是 get_random_sub_rect：

#![allow(unused)]
fn main() {
fn get_random_sub_rect(&self, rect : Rect, rng : &mut RandomNumberGenerator) -> Rect {
    let mut result = rect;
    let rect_width = i32::abs(rect.x1 - rect.x2);
    let rect_height = i32::abs(rect.y1 - rect.y2);

    let w = i32::max(3, rng.roll_dice(1, i32::min(rect_width, 10))-1) + 1;
    let h = i32::max(3, rng.roll_dice(1, i32::min(rect_height, 10))-1) + 1;

    result.x1 += rng.roll_dice(1, 6)-1;
    result.y1 += rng.roll_dice(1, 6)-1;
    result.x2 = result.x1 + w;
    result.y2 = result.y1 + h;

    result
}
}

因此，它以一个矩形作为参数，并制作一个可变副本作为结果使用。它计算矩形的宽度和高度，然后在该矩形内生成一个随机宽度和高度 - 但每个维度都不小于 3 个图块且不大于 10 个图块。您可以调整这些数字以更改您想要的房间大小。然后它稍微移动矩形，以提供一些随机放置（否则，它将始终靠在子矩形的侧面）。最后，它返回结果。图形化表示：

###############        ########
#             #        #   1  #
#             #        #      #
#      0      #   ->   ########
#             #
#             #
###############

最后，是 is_possible 函数：

#![allow(unused)]
fn main() {
fn is_possible(&self, rect : Rect) -> bool {
    let mut expanded = rect;
    expanded.x1 -= 2;
    expanded.x2 += 2;
    expanded.y1 -= 2;
    expanded.y2 += 2;

    let mut can_build = true;

    for y in expanded.y1 ..= expanded.y2 {
        for x in expanded.x1 ..= expanded.x2 {
            if x > self.map.width-2 { can_build = false; }
            if y > self.map.height-2 { can_build = false; }
            if x < 1 { can_build = false; }
            if y < 1 { can_build = false; }
            if can_build {
                let idx = self.map.xy_idx(x, y);
                if self.map.tiles[idx] != TileType::Wall {
                    can_build = false;
                }
            }
        }
    }

    can_build
}
}

这稍微复杂一些，但当您分解它时，它就变得有意义了：

以一个矩形作为目标，表示我们正在查看的房间。
创建一个名为 expanded 的矩形的可变副本。然后我们在每个方向上将矩形向外扩展 2 个图块，以防止房间重叠。
我们迭代矩形中的每个 x 和 y 坐标：
1. 如果 x 或 y 超出地图边界，我们将 can_build 标记为 false - 这将不起作用。
2. 如果我们仍然可以构建它，我们会查看现有地图 - 如果它不是实心墙，那么我们已经与现有房间重叠，并标记为我们无法构建。
我们返回 can_build 的结果。

因此，现在我们已经实现了所有这些，整体算法就更加明显了：

我们从覆盖整个地图的单个矩形开始。
我们对其进行细分，因此现在我们的地图有 5 个矩形 - 每个象限一个，整个地图一个。
我们使用一个计数器来确保我们不会永远循环（我们将拒绝很多房间）。当我们仍然可以添加房间时，我们：
1. 从矩形列表中获取一个随机矩形。最初，这将是象限之一 - 或整个地图。当我们添加细分时，此列表将继续增长。
2. 我们在这个矩形内生成一个随机子矩形。
3. 我们查看这是否是一个可能的房间。如果是，我们：
  1. 将房间应用到地图（构建它）。
  2. 将其添加到房间列表。
  3. 将新的矩形细分为象限，并将这些象限添加到我们的矩形列表。
  4. 存储一个快照以用于可视化工具。

这往往会给出很好的房间分布，并且保证它们不会重叠。非常像 Nethack！

如果您现在 cargo run，您将身处一个没有出口的房间。您将可以在可视化工具中观看房间在地图周围出现。这是一个好的开始。

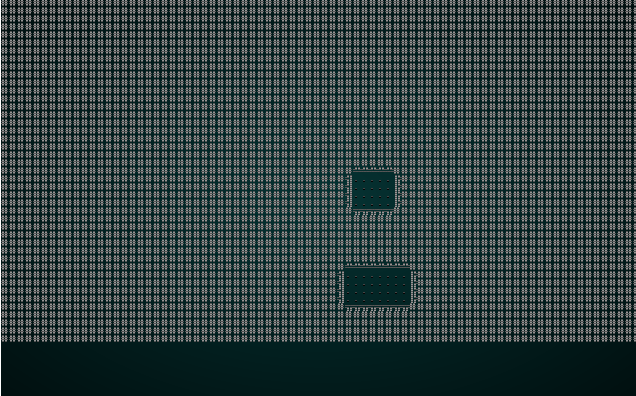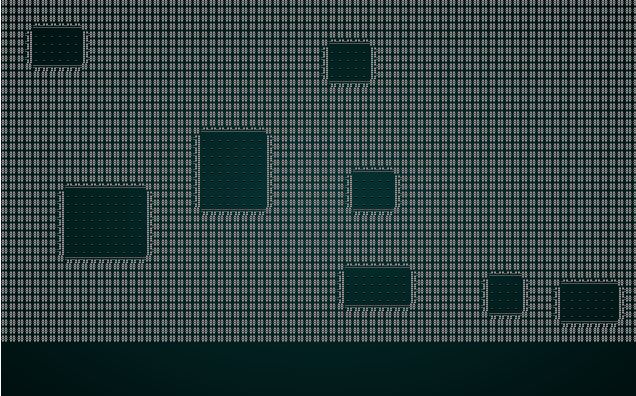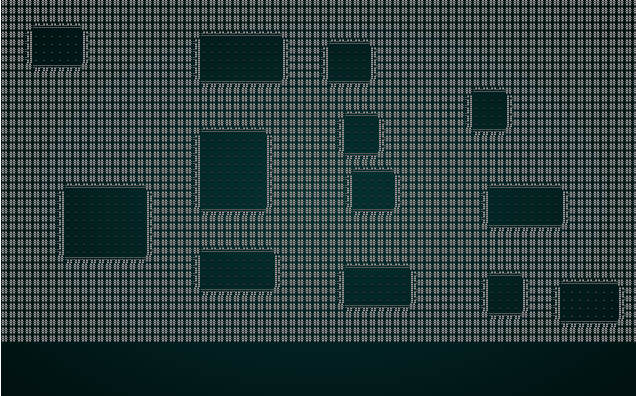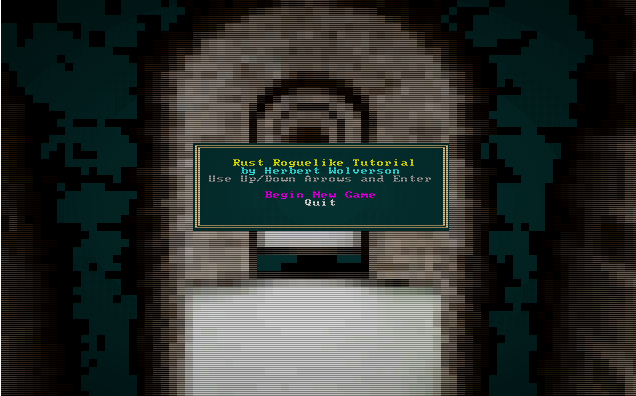
Screenshot

添加走廊

现在，我们按左侧坐标对房间进行排序。您不必这样做，但这有助于使连接的房间对齐。

#![allow(unused)]
fn main() {
self.rooms.sort_by(|a,b| a.x1.cmp(&b.x1) );
}

sort_by 接受一个闭包 - 也就是一个内联函数（在其他语言中称为“lambda”或“匿名函数”）作为参数。如果您愿意，您可以指定另一个完整的函数，或者在 Rect 上实现特征使其可排序 - 但这已经足够容易了。它通过比较每个矩形的 x1 值进行排序。

现在我们将添加一些走廊：

#![allow(unused)]
fn main() {
// 现在我们需要走廊
for i in 0..self.rooms.len()-1 {
    let room = self.rooms[i];
    let next_room = self.rooms[i+1];
    let start_x = room.x1 + (rng.roll_dice(1, i32::abs(room.x1 - room.x2))-1);
    let start_y = room.y1 + (rng.roll_dice(1, i32::abs(room.y1 - room.y2))-1);
    let end_x = next_room.x1 + (rng.roll_dice(1, i32::abs(next_room.x1 - next_room.x2))-1);
    let end_y = next_room.y1 + (rng.roll_dice(1, i32::abs(next_room.y1 - next_room.y2))-1);
    self.draw_corridor(start_x, start_y, end_x, end_y);
    self.take_snapshot();
}
}

这将迭代房间列表，忽略最后一个房间。它获取当前房间和列表中的下一个房间，并计算每个房间内的随机位置（start_x/start_y 和 end_x/end_y）。然后，它使用这些坐标调用神秘的 draw_corridor 函数。 draw_corridor 添加一条从起点到终点的线，仅使用南北或东西方向（它可以给出 90 度弯曲）。它不会像 Bresenham 算法那样给您一条交错的、难以导航的完美直线。我们还会拍摄快照。

draw_corridor 函数非常简单：

#![allow(unused)]
fn main() {
fn draw_corridor(&mut self, x1:i32, y1:i32, x2:i32, y2:i32) {
    let mut x = x1;
    let mut y = y1;

    while x != x2 || y != y2 {
        if x < x2 {
            x += 1;
        } else if x > x2 {
            x -= 1;
        } else if y < y2 {
            y += 1;
        } else if y > y2 {
            y -= 1;
        }

        let idx = self.map.xy_idx(x, y);
        self.map.tiles[idx] = TileType::Floor;
    }
}
}

它接受一个起点和终点，并创建等于起始位置的可变 x 和 y 变量。然后它一直循环，直到 x 和 y 与直线的终点匹配。对于每次迭代，如果 x 小于结束 x - 它向左移动。如果 x 大于结束 x - 它向右移动。 y 也是如此，但方向是向上和向下。这给出了带有单个拐角的直走廊。

别忘了楼梯（我差点忘了！）

最后，我们需要完成并创建出口：

#![allow(unused)]
fn main() {
// 别忘了楼梯
let stairs = self.rooms[self.rooms.len()-1].center();
let stairs_idx = self.map.xy_idx(stairs.0, stairs.1);
self.map.tiles[stairs_idx] = TileType::DownStairs;
}

我们将出口放置在最后一个房间中，以确保可怜的玩家有路可走。

如果您现在 cargo run，您将看到类似这样的内容：

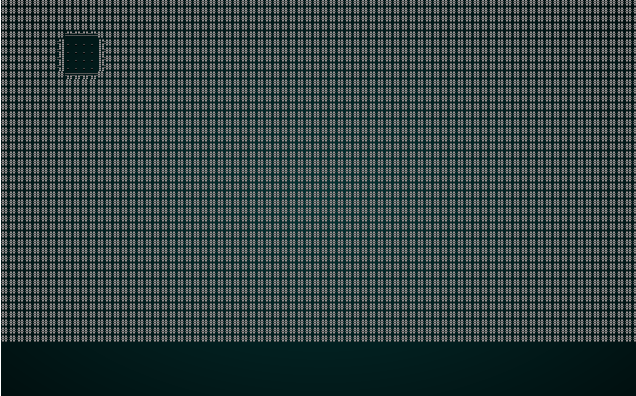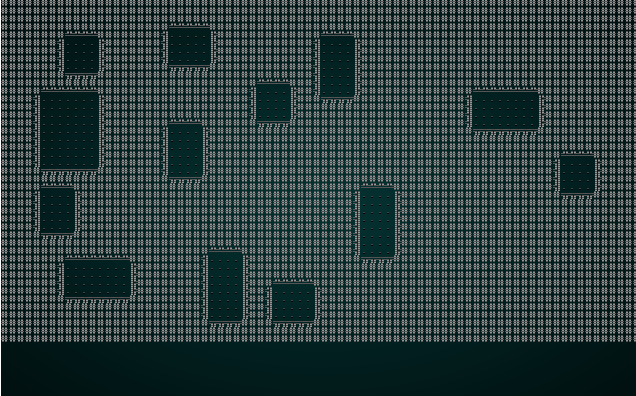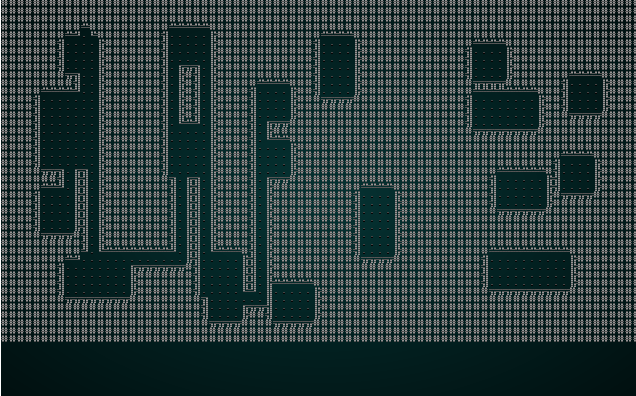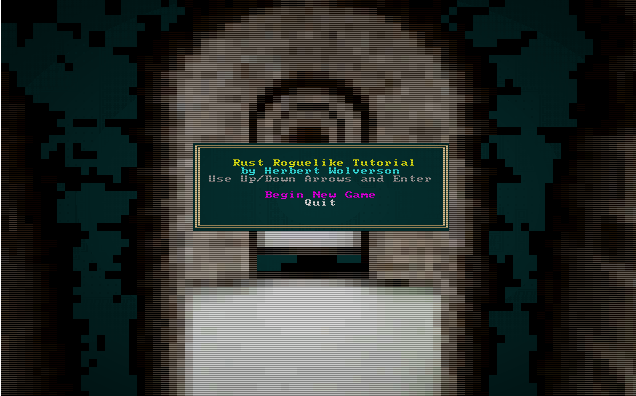Screenshot .

随机化每个地牢关卡

我们希望有时使用其中一种算法，而不是总是使用 BSP 下水道算法。在 map_builders/mod.rs 中，替换 build 函数：

#![allow(unused)]
fn main() {
pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> {
    let mut rng = rltk::RandomNumberGenerator::new();
    let builder = rng.roll_dice(1, 2);
    match builder {
        1 => Box::new(BspDungeonBuilder::new(new_depth)),
        _ => Box::new(SimpleMapBuilder::new(new_depth))
    }
}
}

现在，当您玩游戏时，遇到哪种类型的地图就像掷硬币一样。这些类型的 spawn 函数是相同的 - 因此在下一章之前，我们不会担心地图构建器状态。

总结

您已将地图构建重构为一个新模块，并构建了一个基于简单的 BSP（二叉空间分割）的地图。游戏会随机选择地图类型，并且您拥有更多种类。下一章将进一步重构地图生成，并介绍另一种技术。

本章的源代码可以在这里找到

使用 Rust 开发肉鸽游戏教程