波函数坍缩
关于本教程
本教程是免费且开源的,所有代码均使用 MIT 许可证 - 因此您可以随意使用。 我希望您会喜欢本教程,并制作出色的游戏!
如果您喜欢这个教程并希望我继续写作,请考虑支持 我的 Patreon。
几年前,波函数坍缩 (WFC) 在程序化生成领域引起了轰动。 它看似神奇,可以输入图像 - 并生成类似的图像。 演示表明它可以生成外观精美的游戏关卡,而令人惊叹的《Qud 的洞穴》开始使用它来生成有趣的关卡。 规范的演示 - 以及最初的 C# 算法和各种解释链接/移植版本 - 可以在这里找到。
在本章中,我们将从头开始实现波函数坍缩 - 并将其应用于制作有趣的 Roguelike 关卡。 请注意,有一个包含原始算法的 crate 可用(wfc,以及 wfc-image); 在测试中它看起来相当不错,但我在使其与 WebAssembly 协同工作时遇到了问题。 我也不认为仅仅说“导入这个”就能真正教会算法。 这是一个较长的章节,但到最后您应该对该算法感到满意。
WFC 真正做了什么?
波函数坍缩与我们到目前为止使用的地图生成算法不同,因为它实际上并不制作地图。 它接收源数据(我们将使用其他地图!),扫描它们,并构建一个以完全来自源数据的元素为特征的新地图。 它分几个阶段运行:
- 它读取传入的数据。 在最初的实现中,这是一个 PNG 文件。 在我们的实现中,这是一个像我们之前使用过的
Map结构; 我们还将实现一个 REX Paint 读取器来加载地图。 - 它将源图像划分为“瓦片”(tiles),并且可以选择通过沿一个或两个轴镜像读取的瓦片来制作更多瓦片。
- 它加载或构建一个“约束”图。 这是一组规则,指定哪些瓦片可以彼此相邻。 在图像中,这可以从瓦片邻接关系中推导出来。 在 Roguelike 地图中,出口的连通性是一个很好的指标。 对于基于瓦片的游戏,您可以仔细构建一个布局,说明什么可以放在哪里。
- 然后,它将输出图像划分为瓦片大小的块,并将它们全部设置为“空”。 第一个放置的瓦片将非常随机,然后它选择区域并检查已经已知的瓦片数据 - 放置与已存在瓦片兼容的瓦片。 最终,它放置了所有瓦片 - 您就得到了一张地图/图像!
“波函数坍缩”这个名称指的是量子物理学的思想,即粒子在您观察它之前可能实际上没有状态。 在算法中,瓦片在您选择一个进行检查之前,实际上并不会合并成存在。 因此,与量子物理学有轻微的相似之处。 然而,实际上 - 这个名字是营销的胜利。 该算法被称为 求解器 - 给定一组约束,它迭代可能的解决方案,直到约束被解决。 这不是一个新概念 - Prolog 是一种完全基于这个思想的编程语言,它于 1972 年首次问世。 所以在某种程度上,它比我还老!
入门:Rust 对复杂模块的支持
我们之前的所有算法都足够小,可以放入一个源代码文件中,而无需太多翻页来查找相关的代码片段。 波函数坍缩足够复杂,值得分解成多个文件 - 与 map_builders 模块分解为 module 的方式非常相似 - WFC 将被划分为它自己的 module。 该模块仍然存在于 map_builders 内部 - 所以在某种程度上它实际上是一个子模块。
Rust 使分解任何模块为多个文件变得非常容易:您在父模块内部创建一个目录,并在其中放置一个名为 mod.rs 的文件。 然后您可以在文件夹中放置更多文件,只要您启用它们(使用 mod myfile)并使用内容(使用 use myfile::MyElement),它的工作方式就像单个文件一样。
因此,要开始,在您的 map_builders 目录中 - 创建一个名为 waveform_collapse 的新目录。 在其中添加一个文件 mod.rs。 您应该有一个如下所示的源代码树:
\ src
\ map_builders
\ waveform_collapse
+ mod.rs
bsp_dungeon.rs
(等等)
main.rs
(等等)
我们将使用类似于之前章节的骨架实现来填充 mod.rs:
#![allow(unused)] fn main() { use super::{MapBuilder, Map, TileType, Position, spawner, SHOW_MAPGEN_VISUALIZER, generate_voronoi_spawn_regions, remove_unreachable_areas_returning_most_distant}; use rltk::RandomNumberGenerator; use specs::prelude::*; pub struct WaveformCollapseBuilder { map : Map, starting_position : Position, depth: i32, history: Vec<Map>, noise_areas : HashMap<i32, Vec<usize>> } impl MapBuilder for WaveformCollapseBuilder { fn get_map(&self) -> Map { self.map.clone() } fn get_starting_position(&self) -> Position { self.starting_position.clone() } fn get_snapshot_history(&self) -> Vec<Map> { self.history.clone() } fn build_map(&mut self) { self.build(); } fn spawn_entities(&mut self, ecs : &mut World) { for area in self.noise_areas.iter() { spawner::spawn_region(ecs, area.1, self.depth); } } fn take_snapshot(&mut self) { if SHOW_MAPGEN_VISUALIZER { let mut snapshot = self.map.clone(); for v in snapshot.revealed_tiles.iter_mut() { *v = true; } self.history.push(snapshot); } } } impl WaveformCollapseBuilder { pub fn new(new_depth : i32) -> WaveformCollapseBuilder { WaveformCollapseBuilder{ map : Map::new(new_depth), starting_position : Position{ x: 0, y : 0 }, depth : new_depth, history: Vec::new(), noise_areas : HashMap::new() } } fn build(&mut self) { let mut rng = RandomNumberGenerator::new(); // TODO: 构建器代码放在这里 // 找到一个起点; 从中间开始向左走,直到找到一个开放的瓦片 self.starting_position = Position{ x: self.map.width / 2, y : self.map.height / 2 }; /*let mut start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); while self.map.tiles[start_idx] != TileType::Floor { self.starting_position.x -= 1; start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); }*/ self.take_snapshot(); // 找到所有我们可以从起点到达的瓦片 let exit_tile = remove_unreachable_areas_returning_most_distant(&mut self.map, start_idx); self.take_snapshot(); // 放置楼梯 self.map.tiles[exit_tile] = TileType::DownStairs; self.take_snapshot(); // 现在我们构建一个噪声地图,供以后在生成实体时使用 self.noise_areas = generate_voronoi_spawn_regions(&self.map, &mut rng); } } }
我们还将修改 map_builders/mod.rs 的 random_builder 函数,使其始终返回我们当前正在开发的算法:
#![allow(unused)] fn main() { pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> { /* let mut rng = rltk::RandomNumberGenerator::new(); let builder = rng.roll_dice(1, 16); match builder { 1 => Box::new(BspDungeonBuilder::new(new_depth)), 2 => Box::new(BspInteriorBuilder::new(new_depth)), 3 => Box::new(CellularAutomataBuilder::new(new_depth)), 4 => Box::new(DrunkardsWalkBuilder::open_area(new_depth)), 5 => Box::new(DrunkardsWalkBuilder::open_halls(new_depth)), 6 => Box::new(DrunkardsWalkBuilder::winding_passages(new_depth)), 7 => Box::new(DrunkardsWalkBuilder::fat_passages(new_depth)), 8 => Box::new(DrunkardsWalkBuilder::fearful_symmetry(new_depth)), 9 => Box::new(MazeBuilder::new(new_depth)), 10 => Box::new(DLABuilder::walk_inwards(new_depth)), 11 => Box::new(DLABuilder::walk_outwards(new_depth)), 12 => Box::new(DLABuilder::central_attractor(new_depth)), 13 => Box::new(DLABuilder::insectoid(new_depth)), 14 => Box::new(VoronoiCellBuilder::pythagoras(new_depth)), 15 => Box::new(VoronoiCellBuilder::manhattan(new_depth)), _ => Box::new(SimpleMapBuilder::new(new_depth)) }*/ Box::new(WaveformCollapseBuilder::new(new_depth)) } }
如果您 cargo run 它,这将给您一张空白地图(全是墙壁) - 但这是一个好的起点。
加载源图像 - REX Paint
您可能还记得在第 2 节 中,我们加载了一个 REX Paint 文件用作主菜单屏幕。 我们将在这里做类似的事情,但我们将把它变成一个可玩的地图。 这是一张刻意奇怪的地图,以帮助说明您可以使用此算法做什么。 这是 REX Paint 中的原始图像:
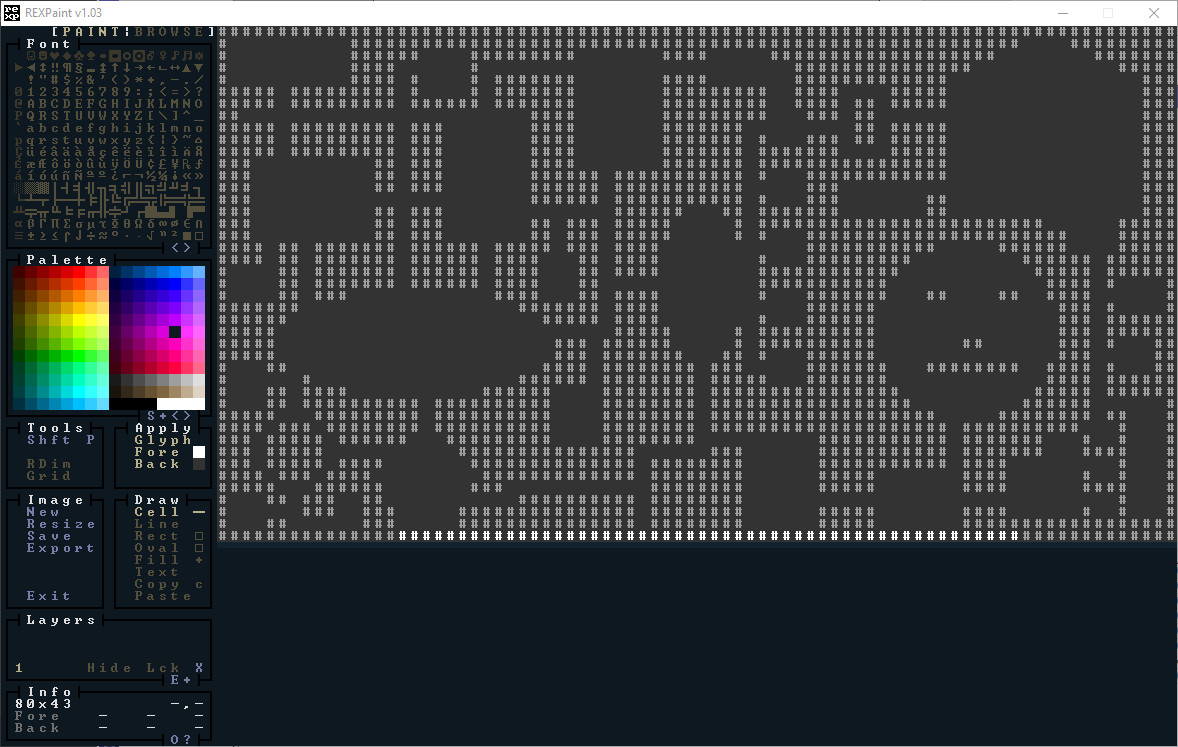 。
。
我尝试包含一些有趣的形状、一张愚蠢的脸以及大量的走廊和不同大小的房间。 这是第二个 REX Paint 文件,旨在更像旧棋盘游戏 The Sorcerer's Cave,该算法让我想起了它 - 具有 1 个出口、2 个出口、3 个出口和 4 个出口的瓦片。 让这些瓦片更漂亮很容易,但为了演示目的,我们将保持简单。
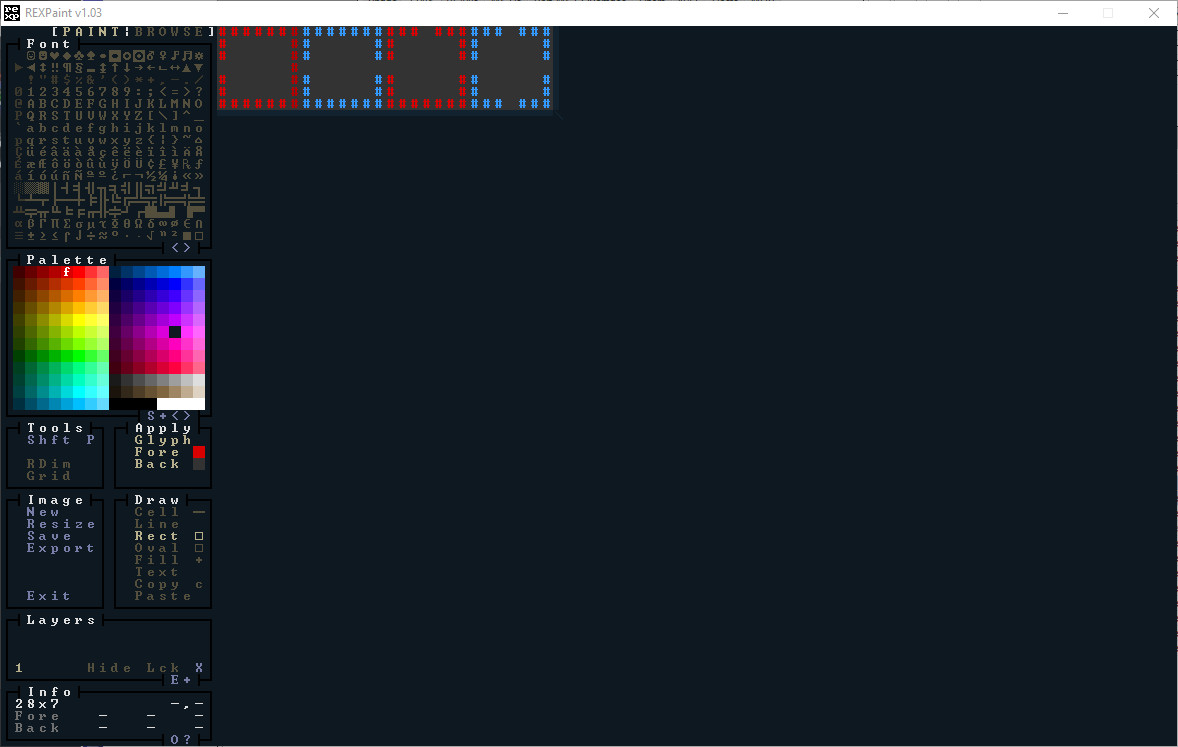 。
。
这些文件位于 resources 目录中,分别为 wfc-demo1.xp 和 wfc-demo2.xp。 我喜欢 REX Paint 的一件事:文件非常小(分别为 102k 和 112k)。 为了使访问它们更容易 - 并避免在发布完成的游戏时必须随可执行文件一起发布它们,我们将它们嵌入到我们的游戏中。 我们之前为主菜单做过这件事。 修改 rex_assets.xp 以包含新文件:
#![allow(unused)] fn main() { use rltk::{rex::XpFile}; rltk::embedded_resource!(SMALL_DUNGEON, "../../resources/SmallDungeon_80x50.xp"); rltk::embedded_resource!(WFC_DEMO_IMAGE1, "../../resources/wfc-demo1.xp"); rltk::embedded_resource!(WFC_DEMO_IMAGE2, "../../resources/wfc-demo2.xp"); pub struct RexAssets { pub menu : XpFile } impl RexAssets { #[allow(clippy::new_without_default)] pub fn new() -> RexAssets { rltk::link_resource!(SMALL_DUNGEON, "../../resources/SmallDungeon_80x50.xp"); rltk::link_resource!(WFC_DEMO_IMAGE1, "../../resources/wfc-demo1.xp"); rltk::link_resource!(WFC_DEMO_IMAGE2, "../../resources/wfc-demo2.xp"); RexAssets{ menu : XpFile::from_resource("../../resources/SmallDungeon_80x50.xp").unwrap() } } } }
最后,我们应该加载地图本身! 在 waveform_collapse 目录中,创建一个新文件:image_loader.rs:
#![allow(unused)] fn main() { use rltk::rex::XpFile; use super::{Map, TileType}; /// 加载 RexPaint 文件,并将其转换为我们的地图格式 pub fn load_rex_map(new_depth: i32, xp_file : &XpFile) -> Map { let mut map : Map = Map::new(new_depth); for layer in &xp_file.layers { for y in 0..layer.height { for x in 0..layer.width { let cell = layer.get(x, y).unwrap(); if x < map.width as usize && y < map.height as usize { let idx = map.xy_idx(x as i32, y as i32); match cell.ch { 32 => map.tiles[idx] = TileType::Floor, // # 35 => map.tiles[idx] = TileType::Wall, // # _ => {} } } } } } map } }
这非常简单,如果您还记得主菜单图形教程,它应该是不言自明的。 此函数:
- 接受
new_depth(因为地图需要它)和对XpFile的引用 - REX Paint 地图的参数。 它将由构造函数完全设置为实体,到处都是墙壁。 - 它使用
new_depth参数创建一个新地图。 - 对于 REX Paint 文件中的每个图层(此时应该只有一个):
- 对于该图层上的每个
y和x:- 加载该坐标的瓦片信息。
- 确保我们在地图边界内(以防尺寸不匹配)。
- 计算单元格的
tiles索引。 - 匹配单元格字形; 如果是
#(35),我们放置一堵墙,如果是空格 (32),我们放置一个地板。
- 对于该图层上的每个
现在我们可以修改我们的 build 函数(在 mod.rs 中)来加载地图:
#![allow(unused)] fn main() { fn build(&mut self) { let mut rng = RandomNumberGenerator::new(); self.map = load_rex_map(self.depth, &rltk::rex::XpFile::from_resource("../../resources/wfc-demo1.xp").unwrap()); self.take_snapshot(); // 找到一个起点; 从中间开始向左走,直到找到一个开放的瓦片 self.starting_position = Position{ x: self.map.width / 2, y : self.map.height / 2 }; ... }
在顶部,我们必须告诉它使用新的 image_loader 文件:
#![allow(unused)] fn main() { mod image_loader; use image_loader::*; }
请注意,我们没有在这些前面加上 pub:我们正在使用它们,但没有在模块外部公开它们。 这有助于我们保持代码的简洁,并缩短我们的编译时间!
就其本身而言,这很酷 - 我们现在可以加载任何 REX Paint 设计的关卡并进行游戏! 如果您现在 cargo run,您会发现您可以玩新地图:
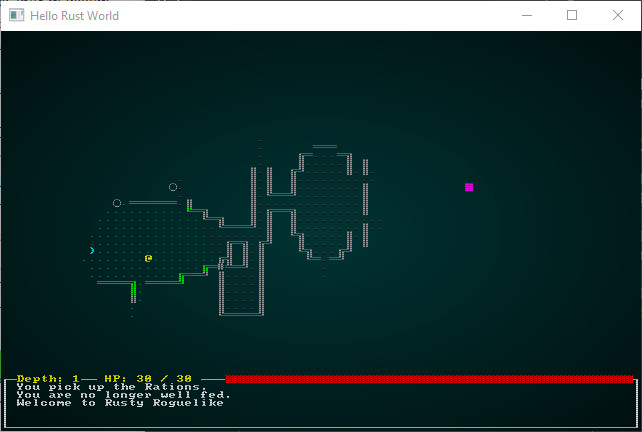 。
。
我们将在后面的章节中利用这一点来制作地窖、预制件和预先设计的关卡 - 但现在,我们只将其用作波函数坍缩实现的后续步骤的源数据。
将我们的地图分割成瓦片
我们之前讨论过 WFC 的工作原理是将原始图像分割成块/瓦片,并可选择地在不同方向上翻转它们。 它这样做是构建约束的第一部分 - 地图如何布局。 所以现在我们需要开始分割我们的图像。
我们将从选择一个瓦片大小开始(我们将其称为 chunk_size)。 我们现在将其设为一个常量(稍后它将变为可调整的),并从大小 7 开始 - 因为这是我们的第二个 REX 演示文件中的瓦片大小。 我们还将调用一个稍后我们将编写的函数:
#![allow(unused)] fn main() { fn build(&mut self) { let mut rng = RandomNumberGenerator::new(); const CHUNK_SIZE :i32 = 7; self.map = load_rex_map(self.depth, &rltk::rex::XpFile::from_resource("../../resources/wfc-demo2.xp").unwrap()); self.take_snapshot(); let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); ... }
由于我们正在处理约束,我们将在我们的 map_builders/waveform_collapse 目录中创建一个新文件 - constraints.rs。 我们将创建一个名为 build_patterns 的函数:
#![allow(unused)] fn main() { use super::{TileType, Map}; use std::collections::HashSet; pub fn build_patterns(map : &Map, chunk_size: i32, include_flipping: bool, dedupe: bool) -> Vec<Vec<TileType>> { let chunks_x = map.width / chunk_size; let chunks_y = map.height / chunk_size; let mut patterns = Vec::new(); for cy in 0..chunks_y { for cx in 0..chunks_x { // 正常方向 let mut pattern : Vec<TileType> = Vec::new(); let start_x = cx * chunk_size; let end_x = (cx+1) * chunk_size; let start_y = cy * chunk_size; let end_y = (cy+1) * chunk_size; for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(x, y); pattern.push(map.tiles[idx]); } } patterns.push(pattern); if include_flipping { // 水平翻转 pattern = Vec::new(); for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(end_x - (x+1), y); pattern.push(map.tiles[idx]); } } patterns.push(pattern); // 垂直翻转 pattern = Vec::new(); for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(x, end_y - (y+1)); pattern.push(map.tiles[idx]); } } patterns.push(pattern); // 同时翻转 pattern = Vec::new(); for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(end_x - (x+1), end_y - (y+1)); pattern.push(map.tiles[idx]); } } patterns.push(pattern); } } } // 去重 if dedupe { rltk::console::log(format!("去重前,有 {} 个模式", patterns.len())); let set: HashSet<Vec<TileType>> = patterns.drain(..).collect(); // 去重 patterns.extend(set.into_iter()); rltk::console::log(format!("有 {} 个模式", patterns.len())); } patterns } }
这是一个相当冗长的函数,所以让我们逐步了解它:
- 在顶部,我们从项目中的其他位置导入了一些项目:
Map、TileType和内置集合HashMap。 - 我们声明了
build_patterns函数,其参数为对源地图的引用、要使用的chunk_size(瓦片大小)以及include_flipping和dedupe的标志(bool变量)。 这些指示我们在读取源地图时希望使用的功能。 我们返回一个vector,其中包含一系列不同的TileType的vector。 外部容器保存每个模式。 内部 vector 保存构成模式本身的TileType。 - 我们确定每个方向有多少块,并将其存储在
chunks_x和chunks_y中。 - 我们创建一个名为
patterns的新vector。 这将保存函数的结果; 我们没有声明它的类型,因为 Rust 足够聪明,可以看到我们将在函数末尾返回它 - 并且可以为我们计算出它的类型。 - 我们迭代变量
cy中的每个垂直块:- 我们迭代变量
cx中的每个水平块:- 我们创建一个新的
vector来保存此模式。 - 我们计算
start_x、end_x、start_y和end_y以保存此块的四个角坐标 - 在原始地图上。 - 我们以
y/x顺序迭代模式(以匹配我们的地图格式),读取块内每个地图瓦片的TileType,并将其添加到模式中。 - 我们将模式推送到
patterns结果 vector。 - 如果
include_flipping设置为true(因为我们想要翻转我们的瓦片,制作更多瓦片!):- 以不同的顺序重复迭代
y/x,给出另外 3 个瓦片。 每个都添加到patterns结果 vector。
- 以不同的顺序重复迭代
- 我们创建一个新的
- 我们迭代变量
- 如果设置了
dedupe,那么我们正在“去重”模式缓冲区。 基本上,删除任何出现多次的模式。 如果地图有很多浪费的空间,而您不想制作同样稀疏的结果地图,这会很有用。 我们通过将模式添加到HashMap(只能存储每个条目的一个)中,然后再将其读出来来去重。
为了使此代码编译,我们必须使 TileType 知道如何将其自身转换为 hash。 HashMap 使用“哈希”(基本上是包含值的校验和)来确定条目是否唯一,并帮助找到它。 在 map.rs 中,我们可以简单地向 TileType 枚举添加一个派生属性:
#![allow(unused)] fn main() { #[derive(PartialEq, Eq, Hash, Copy, Clone, Serialize, Deserialize)] pub enum TileType { Wall, Floor, DownStairs } }
此代码应为您获取源文件中的每个 7x7 瓦片 - 但如果能够证明它有效,那就太好了! 正如里根的演讲稿撰写人曾经写道的那样,信任 - 但要验证。 在 constraints.rs 中,我们将添加另一个函数:render_pattern_to_map:
#![allow(unused)] fn main() { fn render_pattern_to_map(map : &mut Map, pattern: &Vec<TileType>, chunk_size: i32, start_x : i32, start_y: i32) { let mut i = 0usize; for tile_y in 0..chunk_size { for tile_x in 0..chunk_size { let map_idx = map.xy_idx(start_x + tile_x, start_y + tile_y); map.tiles[map_idx] = pattern[i]; map.visible_tiles[map_idx] = true; i += 1; } } } }
这非常简单:迭代模式,并复制到地图上的某个位置 - 由 start_x 和 start_y 坐标偏移。 请注意,我们还将瓦片标记为 visible - 这将使渲染器以彩色显示我们的瓦片。
现在我们只需要显示我们的瓦片作为 snapshot 系统的一部分。 在 waveform_collapse/mod.rs 中,在 WaveformCollapseBuilder 的实现中添加一个新函数(在 build 下面)。 这是一个成员函数,因为它需要访问 take_snapshot 命令:
#![allow(unused)] fn main() { fn render_tile_gallery(&mut self, patterns: &Vec<Vec<TileType>>, chunk_size: i32) { self.map = Map::new(0); let mut counter = 0; let mut x = 1; let mut y = 1; while counter < patterns.len() { render_pattern_to_map(&mut self.map, &patterns[counter], chunk_size, x, y); x += chunk_size + 1; if x + chunk_size > self.map.width { // 移动到下一行 x = 1; y += chunk_size + 1; if y + chunk_size > self.map.height { // 移动到下一页 self.take_snapshot(); self.map = Map::new(0); x = 1; y = 1; } } counter += 1; } self.take_snapshot(); } }
现在,我们需要调用它。 在 build 中:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); self.render_tile_gallery(&patterns, CHUNK_SIZE); }
此外,注释掉一些代码,以免因无法找到起点而崩溃:
#![allow(unused)] fn main() { let mut start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); /*while self.map.tiles[start_idx] != TileType::Floor { self.starting_position.x -= 1; start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); }*/ }
如果您现在 cargo run,它将显示地图示例 2 中的瓦片模式:
 。
。
请注意,翻转如何为我们提供了每个瓦片的多个变体。 如果我们将图像加载代码更改为加载 wfc-demo1(通过将加载器更改为 self.map = load_rex_map(self.depth, &rltk::rex::XpFile::from_resource("../../resources/wfc-demo1.xp").unwrap());),我们将获得手绘地图的块:
 。
。
构建约束矩阵
现在我们需要开始告诉算法如何将瓦片彼此相邻放置。 我们可以采用简单的“原始图像上与它相邻的是什么?”算法,但这会忽略 Roguelike 地图中的一个关键因素:连通性。 与整体美学相比,我们更关注从点 A 到点 B 的能力! 所以我们需要编写一个约束构建器,它考虑到连通性。
我们将首先扩展 mod.rs 中的 builder 以调用一个假设的函数,我们将在稍后实现它:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); self.render_tile_gallery(&patterns, CHUNK_SIZE); let constraints = patterns_to_constraints(patterns, CHUNK_SIZE); }
这为我们提供了一个新方法 patterns_to_constraints 的签名,以添加到 constraints.rs。 我们还需要一个新的类型和一个辅助函数。 我们将在其他地方使用这些,因此我们将在 waveform_collapse 文件夹中添加一个新文件 - common.rs。
#![allow(unused)] fn main() { use super::TileType; #[derive(PartialEq, Eq, Hash, Clone)] pub struct MapChunk { pub pattern : Vec<TileType>, pub exits: [Vec<bool>; 4], pub has_exits: bool, pub compatible_with: [Vec<usize>; 4] } pub fn tile_idx_in_chunk(chunk_size: i32, x:i32, y:i32) -> usize { ((y * chunk_size) + x) as usize } }
我们将 MapChunk 定义为一个结构体,包含实际模式、出口结构(稍后详细介绍)、一个 bool 值来说明我们是否有任何出口,以及一个名为 compatible_with 的结构(稍后也会详细介绍)。 我们还定义了 tile_idx_in_chunk - 它就像 map.xy_idx - 但限制为小瓦片类型。
现在我们将在 constraints.rs 中编写 patterns_to_constraints:
#![allow(unused)] fn main() { pub fn patterns_to_constraints(patterns: Vec<Vec<TileType>>, chunk_size : i32) -> Vec<MapChunk> { // 移动到新的约束对象中 let mut constraints : Vec<MapChunk> = Vec::new(); for p in patterns { let mut new_chunk = MapChunk{ pattern: p, exits: [ Vec::new(), Vec::new(), Vec::new(), Vec::new() ], has_exits : true, compatible_with: [ Vec::new(), Vec::new(), Vec::new(), Vec::new() ] }; for exit in new_chunk.exits.iter_mut() { for _i in 0..chunk_size { exit.push(false); } } let mut n_exits = 0; for x in 0..chunk_size { // 检查北向出口 let north_idx = tile_idx_in_chunk(chunk_size, x, 0); if new_chunk.pattern[north_idx] == TileType::Floor { new_chunk.exits[0][x as usize] = true; n_exits += 1; } // 检查南向出口 let south_idx = tile_idx_in_chunk(chunk_size, x, chunk_size-1); if new_chunk.pattern[south_idx] == TileType::Floor { new_chunk.exits[1][x as usize] = true; n_exits += 1; } // 检查西向出口 let west_idx = tile_idx_in_chunk(chunk_size, 0, x); if new_chunk.pattern[west_idx] == TileType::Floor { new_chunk.exits[2][x as usize] = true; n_exits += 1; } // 检查东向出口 let east_idx = tile_idx_in_chunk(chunk_size, chunk_size-1, x); if new_chunk.pattern[east_idx] == TileType::Floor { new_chunk.exits[3][x as usize] = true; n_exits += 1; } } if n_exits == 0 { new_chunk.has_exits = false; } constraints.push(new_chunk); } // 构建兼容性矩阵 let ch = constraints.clone(); for c in constraints.iter_mut() { for (j,potential) in ch.iter().enumerate() { // 如果根本没有出口,则兼容 if !c.has_exits || !potential.has_exits { for compat in c.compatible_with.iter_mut() { compat.push(j); } } else { // 按方向评估兼容性 for (direction, exit_list) in c.exits.iter_mut().enumerate() { let opposite = match direction { 0 => 1, // 我们的北,他们的南 1 => 0, // 我们的南,他们的北 2 => 3, // 我们的西,他们的东 _ => 2 // 我们的东,他们的西 }; let mut it_fits = false; let mut has_any = false; for (slot, can_enter) in exit_list.iter().enumerate() { if *can_enter { has_any = true; if potential.exits[opposite][slot] { it_fits = true; } } } if it_fits { c.compatible_with[direction].push(j); } if !has_any { // 这边没有出口,我们不在乎那里放什么 for compat in c.compatible_with.iter_mut() { compat.push(j); } } } } } } constraints } }
这是一个非常大的函数,但显然被分解为多个部分。 让我们花时间逐步了解它实际做了什么:
- 它接受第一个参数
patterns作为Vec<Vec<TileType>>- 我们用来构建模式的类型。 第二个参数chunk_size与我们之前使用的相同。 它返回新MapChunk类型的vector。MapChunk是一个模式,但添加了额外的出口和兼容性信息。 因此,我们承诺,给定一组模式图形,我们将添加所有导航信息并以一组块的形式返回模式。 - 它创建一个名为
constraints的MapChunk类型的Vec。 这是我们的结果 - 我们将在其中添加内容,并在最后将其返回给调用者。 - 现在我们迭代
patterns中的每个模式,称之为p(以节省输入)。 对于每个模式:- 我们创建一个新的
MapChunk。pattern字段获取我们模式的副本。exits是一个数组(固定大小的集合;在本例中大小为 4)的 vector,因此我们向其中插入 4 个空 vector。compatible_with也是一个 vector 数组,因此我们将它们设置为新的 - 空 - vector。 我们将has_exits设置为true- 我们稍后会设置它。 - 我们从 0 迭代到
chunk_size,并在新地图块的每个exits字段中添加false。exits结构表示每个可能的方向(北、南、西、东)一个条目 - 因此它需要每个块大小一个条目来表示该方向的每个可能的出口瓦片。 我们稍后将检查实际的连通性 - 现在,我们只是想要每个方向的占位符。 - 我们将
n_exits设置为 0,并使其为可变的 - 以便我们稍后可以添加到其中。 我们将在整个过程中计算出口总数。 - 我们迭代
x从 0 到chunk_size,对于每个x值:- 我们检查北向出口。 这些出口始终位于块内的
(x, 0)位置 - 因此我们计算要检查的瓦片索引为tile_idx_in_chunk(chunk_size, x, 0)。 如果该瓦片是地板,我们将在n_exits中加一,并将new_chunk.exits[0][x]设置为true。 - 我们对南向出口执行相同的操作。 这些出口始终位于
(x, chunk_size-1)位置,因此我们计算块索引为tile_idx_in_chunk(chunk_size, x, chunk_size-1)。 如果该瓦片是地板,我们将在n_exits中加一,并将new_chunks.exits[1][x]设置为true。 - 我们再次对西向出口执行相同的操作,西向出口位于
(0,x)位置。 - 我们再次对东向出口执行相同的操作,东向出口位于
(chunk_size-1,0)位置。
- 我们检查北向出口。 这些出口始终位于块内的
- 如果
n_exits为 0,我们将new_chunk.has_exits设置为 0 - 没有进出此块的方式! - 我们将
new_chunk推送到constraints结果 vector。
- 我们创建一个新的
- 现在是构建兼容性矩阵的时候了! 这里的想法是通过匹配相邻边缘的出口来匹配哪些瓦片可以放置到哪些其他瓦片。
- 为了避免借用检查器问题,我们使用
let ch = constraints.clone();获取现有约束的副本。 Rust 不太喜欢同时从同一个vector读取和写入 - 因此这避免了我们必须进行舞蹈以保持其分离。 - 对于结果 vector
constraints中的每个constraint,命名为c,我们:- 将
ch中的每个约束迭代为potential,这是约束 vector 的副本。 我们添加一个枚举器j来告诉我们它的索引方式。- 如果
c(我们正在编辑的约束)和potential(我们正在检查的约束)都没有出口,那么我们使其与所有内容兼容。 我们这样做是为了增加成功解决地图并仍然包含这些瓦片的机会(否则,它们将永远不会被选中)。 为了增加与所有内容的兼容性,我们将j添加到所有四个方向的compatibile_with结构中。 因此,c可以与potential在任何方向上相邻放置。 - 否则,我们迭代
c上的所有四个出口方向:- 我们将
opposite设置为我们正在评估的方向的倒数; 因此,北变为南,东变为西,等等。 - 我们设置两个可变变量
it_fits和has_any- 并将它们都设置为false。 我们将在后续步骤中使用这些变量。it_fits表示c的出口瓦片和potential的入口瓦片之间存在一个或多个匹配的出口。has_any表示c在此方向上是否有任何出口。 我们区分这两者是因为如果该方向上没有出口,我们不在乎邻居是什么 - 我们无法影响它。 如果有出口,那么我们只希望与您实际可以访问的瓦片兼容。 - 我们迭代
c的 exits,同时保留一个slot(我们正在评估的瓦片编号)和exit瓦片的值 (can_enter)。 您会记得,如果它们是地板,我们将这些设置为true- 否则设置为false- 因此我们正在迭代可能的出口。- 如果
can_enter为true,那么我们将has_any设置为 true - 它在该方向上有一个出口。 - 我们检查
potential_exits.exits[opposite][slot]- 即另一个瓦片上的匹配出口,方向与我们前进的方向相反。 如果存在匹配,那么您可以从瓦片c到瓦片potential在我们当前的方向上! 这使我们可以将it_fits设置为 true。
- 如果
- 如果
it_fits为true,则瓦片之间存在兼容性:我们将j添加到c的compatible_withvector 中,用于当前方向。 - 如果
has_any为false,那么我们不在乎此方向上的邻接关系 - 因此我们将j添加到所有方向的兼容性矩阵中,就像我们对没有出口的瓦片所做的那样。
- 我们将
- 如果
- 将
- 最后,我们返回我们的
constraints结果 vector。
这是一个相当复杂的算法,因此我们真的不想相信我做对了。 我们将通过调整我们的瓦片画廊代码来显示出口来验证出口检测。 在 build 中,调整渲染顺序以及我们传递给 render_tile_gallery 的内容:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); let constraints = patterns_to_constraints(patterns, CHUNK_SIZE); self.render_tile_gallery(&constraints, CHUNK_SIZE); }
我们还需要修改 render_tile_gallery:
#![allow(unused)] fn main() { fn render_tile_gallery(&mut self, constraints: &Vec<MapChunk>, chunk_size: i32) { self.map = Map::new(0); let mut counter = 0; let mut x = 1; let mut y = 1; while counter < constraints.len() { render_pattern_to_map(&mut self.map, &constraints[counter], chunk_size, x, y); x += chunk_size + 1; if x + chunk_size > self.map.width { // 移动到下一行 x = 1; y += chunk_size + 1; if y + chunk_size > self.map.height { // 移动到下一页 self.take_snapshot(); self.map = Map::new(0); x = 1; y = 1; } } counter += 1; } self.take_snapshot(); } }
这要求我们也修改我们的 render_pattern_to_map 函数:
#![allow(unused)] fn main() { pub fn render_pattern_to_map(map : &mut Map, chunk: &MapChunk, chunk_size: i32, start_x : i32, start_y: i32) { let mut i = 0usize; for tile_y in 0..chunk_size { for tile_x in 0..chunk_size { let map_idx = map.xy_idx(start_x + tile_x, start_y + tile_y); map.tiles[map_idx] = chunk.pattern[i]; map.visible_tiles[map_idx] = true; i += 1; } } for (x,northbound) in chunk.exits[0].iter().enumerate() { if *northbound { let map_idx = map.xy_idx(start_x + x as i32, start_y); map.tiles[map_idx] = TileType::DownStairs; } } for (x,southbound) in chunk.exits[1].iter().enumerate() { if *southbound { let map_idx = map.xy_idx(start_x + x as i32, start_y + chunk_size -1); map.tiles[map_idx] = TileType::DownStairs; } } for (x,westbound) in chunk.exits[2].iter().enumerate() { if *westbound { let map_idx = map.xy_idx(start_x, start_y + x as i32); map.tiles[map_idx] = TileType::DownStairs; } } for (x,eastbound) in chunk.exits[3].iter().enumerate() { if *eastbound { let map_idx = map.xy_idx(start_x + chunk_size - 1, start_y + x as i32); map.tiles[map_idx] = TileType::DownStairs; } } } }
现在我们已经运行了演示框架,我们可以 cargo run 项目 - 并看到 wfc-demo2.xp 中的瓦片正确突出显示了出口:
 。
。
wfc-demo1.xp 出口也突出显示:
 。
。
太棒了! 我们的出口查找器工作正常。
构建求解器
您还记得过去在长途旅行中可以买到的旧逻辑问题书吗? “弗雷德是律师,玛丽是医生,吉姆失业了。 弗雷德不能坐在失业者旁边,因为他很势利。 玛丽喜欢所有人。 你应该如何安排他们的座位?” 这是一个约束问题的示例,求解器旨在帮助解决这类问题。 构建我们的地图没有什么不同 - 我们正在读取约束矩阵(我们在上面构建的矩阵)以确定我们可以在任何给定区域放置哪些瓦片。 因为它是 Roguelike 游戏,并且我们希望每次都有不同的东西,所以我们想要注入一些随机性 - 并每次都获得不同但有效的地图。
让我们扩展我们的 build 函数以调用一个假设的求解器:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); let constraints = patterns_to_constraints(patterns, CHUNK_SIZE); self.render_tile_gallery(&constraints, CHUNK_SIZE); self.map = Map::new(self.depth); loop { let mut solver = Solver::new(constraints.clone(), CHUNK_SIZE, &self.map); while !solver.iteration(&mut self.map, &mut rng) { self.take_snapshot(); } self.take_snapshot(); if solver.possible { break; } // 如果它遇到了不可能的条件,请重试 } }
我们制作了一张全新的实体地图(因为我们一直在使用它来渲染瓦片演示,并且不想用演示画廊污染最终地图!)。 然后我们 loop(Rust 循环,除非某些东西调用 break,否则永远运行)。 在该循环中,我们为 constraints 矩阵的副本创建一个求解器(我们复制它是为了以防我们必须重复执行;否则,我们将不得不 move 它进入并再次 move 它出来)。 我们重复调用求解器的 iteration 函数,每次都拍摄快照 - 直到它报告完成为止。 如果 solver 放弃并说不可能,我们重试。
我们将首先在我们的 waveform_collapse 目录中添加 solver.rs。 求解器需要保持自己的状态:也就是说,当它迭代时,它需要知道它已经走了多远。 我们将通过将 Solver 转换为结构体来支持这一点:
#![allow(unused)] fn main() { pub struct Solver { constraints: Vec<MapChunk>, chunk_size : i32, chunks : Vec<Option<usize>>, chunks_x : usize, chunks_y : usize, remaining : Vec<(usize, i32)>, // (索引,# 邻居) pub possible: bool } }
它存储了我们一直在构建的 constraints、我们正在使用的 chunk_size、我们正在解析的 chunks(稍后详细介绍)、它可以容纳在目标地图上的块数(chunks_x 和 chunks_y)、一个 remaining 向量(稍后也会详细介绍),以及一个 possible 指示器,用于指示它是否放弃。
chunks 是 Option<usize> 的 vector。 usize 值是块的索引。 它是一个选项,因为我们可能还没有填写它 - 因此它可能是 None 或 Some(usize)。 这很好地表示了问题的“量子波函数坍缩”性质 - 它要么存在,要么不存在,在我们看到它之前我们不知道!
remaining 是所有块的 vector,带有它们的索引。 这是一个 tuple - 我们将块索引存储在第一个条目中,并将现有邻居的数量存储在第二个条目中。 我们将使用它来帮助决定接下来要填充哪个块,并在添加一个块后将其从 remaining 列表中删除。
我们还需要为 Solver 实现方法。 new 是一个基本的构造函数:
#![allow(unused)] fn main() { impl Solver { pub fn new(constraints: Vec<MapChunk>, chunk_size: i32, map : &Map) -> Solver { let chunks_x = (map.width / chunk_size) as usize; let chunks_y = (map.height / chunk_size) as usize; let mut remaining : Vec<(usize, i32)> = Vec::new(); for i in 0..(chunks_x*chunks_y) { remaining.push((i, 0)); } Solver { constraints, chunk_size, chunks: vec![None; chunks_x * chunks_y], chunks_x, chunks_y, remaining, possible: true } } ... }
它计算大小(对于 chunks_x 和 chunks_y),用每个瓦片和没有邻居的值填充 remaining,并用 None 值填充 chunks。 这为我们的求解运行做好了准备! 我们还需要一个名为 chunk_idx 的辅助函数:
#![allow(unused)] fn main() { fn chunk_idx(&self, x:usize, y:usize) -> usize { ((y * self.chunks_x) + x) as usize } }
这很像 map 中的 xy_idx,或 common 中的 tile_idx_in_chunk - 但受到我们可以容纳在地图上的块数的限制。 我们还将依赖 count_neighbors:
#![allow(unused)] fn main() { fn count_neighbors(&self, chunk_x:usize, chunk_y:usize) -> i32 { let mut neighbors = 0; if chunk_x > 0 { let left_idx = self.chunk_idx(chunk_x-1, chunk_y); match self.chunks[left_idx] { None => {} Some(_) => { neighbors += 1; } } } if chunk_x < self.chunks_x-1 { let right_idx = self.chunk_idx(chunk_x+1, chunk_y); match self.chunks[right_idx] { None => {} Some(_) => { neighbors += 1; } } } if chunk_y > 0 { let up_idx = self.chunk_idx(chunk_x, chunk_y-1); match self.chunks[up_idx] { None => {} Some(_) => { neighbors += 1; } } } if chunk_y < self.chunks_y-1 { let down_idx = self.chunk_idx(chunk_x, chunk_y+1); match self.chunks[down_idx] { None => {} Some(_) => { neighbors += 1; } } } neighbors } }
这个函数可以小很多,但我把它留下来是为了清楚地说明每一步。 它查看一个块,并确定它是否在北、南、东和西方向上有一个已创建(未设置为 None)的块。
最后,我们得到了 iteration 函数 - 它完成了繁重的工作:
#![allow(unused)] fn main() { pub fn iteration(&mut self, map: &mut Map, rng : &mut super::RandomNumberGenerator) -> bool { if self.remaining.is_empty() { return true; } // 填充剩余列表的邻居计数 let mut remain_copy = self.remaining.clone(); let mut neighbors_exist = false; for r in remain_copy.iter_mut() { let idx = r.0; let chunk_x = idx % self.chunks_x; let chunk_y = idx / self.chunks_x; let neighbor_count = self.count_neighbors(chunk_x, chunk_y); if neighbor_count > 0 { neighbors_exist = true; } *r = (r.0, neighbor_count); } remain_copy.sort_by(|a,b| b.1.cmp(&a.1)); self.remaining = remain_copy; // 选择一个我们尚未处理的随机块并获取其索引,从剩余列表中删除 let remaining_index = if !neighbors_exist { (rng.roll_dice(1, self.remaining.len() as i32)-1) as usize } else { 0usize }; let chunk_index = self.remaining[remaining_index].0; self.remaining.remove(remaining_index); let chunk_x = chunk_index % self.chunks_x; let chunk_y = chunk_index / self.chunks_x; let mut neighbors = 0; let mut options : Vec<Vec<usize>> = Vec::new(); if chunk_x > 0 { let left_idx = self.chunk_idx(chunk_x-1, chunk_y); match self.chunks[left_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[3].clone()); } } } if chunk_x < self.chunks_x-1 { let right_idx = self.chunk_idx(chunk_x+1, chunk_y); match self.chunks[right_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[2].clone()); } } } if chunk_y > 0 { let up_idx = self.chunk_idx(chunk_x, chunk_y-1); match self.chunks[up_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[1].clone()); } } } if chunk_y < self.chunks_y-1 { let down_idx = self.chunk_idx(chunk_x, chunk_y+1); match self.chunks[down_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[0].clone()); } } } if neighbors == 0 { // 附近没有任何东西,所以我们可以拥有任何东西! let new_chunk_idx = (rng.roll_dice(1, self.constraints.len() as i32)-1) as usize; self.chunks[chunk_index] = Some(new_chunk_idx); let left_x = chunk_x as i32 * self.chunk_size as i32; let right_x = (chunk_x as i32+1) * self.chunk_size as i32; let top_y = chunk_y as i32 * self.chunk_size as i32; let bottom_y = (chunk_y as i32+1) * self.chunk_size as i32; let mut i : usize = 0; for y in top_y .. bottom_y { for x in left_x .. right_x { let mapidx = map.xy_idx(x, y); let tile = self.constraints[new_chunk_idx].pattern[i]; map.tiles[mapidx] = tile; i += 1; } } } else { // 附近有邻居,所以我们尝试与它们兼容 let mut options_to_check : HashSet<usize> = HashSet::new(); for o in options.iter() { for i in o.iter() { options_to_check.insert(*i); } } let mut possible_options : Vec<usize> = Vec::new(); for new_chunk_idx in options_to_check.iter() { let mut possible = true; for o in options.iter() { if !o.contains(new_chunk_idx) { possible = false; } } if possible { possible_options.push(*new_chunk_idx); } } if possible_options.is_empty() { rltk::console::log("哦不! 这不可能!"); self.possible = false; return true; } else { let new_chunk_idx = if possible_options.len() == 1 { 0 } else { rng.roll_dice(1, possible_options.len() as i32)-1 }; self.chunks[chunk_index] = Some(new_chunk_idx as usize); let left_x = chunk_x as i32 * self.chunk_size as i32; let right_x = (chunk_x as i32+1) * self.chunk_size as i32; let top_y = chunk_y as i32 * self.chunk_size as i32; let bottom_y = (chunk_y as i32+1) * self.chunk_size as i32; let mut i : usize = 0; for y in top_y .. bottom_y { for x in left_x .. right_x { let mapidx = map.xy_idx(x, y); let tile = self.constraints[new_chunk_idx as usize].pattern[i]; map.tiles[mapidx] = tile; i += 1; } } } } false } }
这是另一个非常大的函数,但同样是因为我试图使其易于阅读。 让我们逐步了解算法:
- 如果
remaining中没有任何剩余内容,我们返回表明我们已完成地图。possible为真,因为我们实际上完成了问题。 - 我们获取
remaining的clone以避免借用检查器问题。 - 我们迭代
remaining的副本,对于每个剩余的块:- 我们从块索引确定它的
x和y位置。 - 我们调用
count_neighbors以确定有多少(如果有)相邻块已被解析。 - 如果找到任何邻居,我们将
neighbors_exist设置为 true - 告诉算法它至少运行了一次。 - 我们更新
remaining列表的副本,以包含与之前相同的索引和新的邻居计数。
- 我们从块索引确定它的
- 我们按邻居数量降序对
remaining的副本进行排序 - 因此邻居最多的块排在第一位。 - 我们将
remaining的克隆副本复制回我们的实际remaining列表。 - 我们想要创建一个新变量
remaining_index- 以指示我们要处理哪个块,以及它在remainingvector 中的位置。 如果我们还没有制作任何瓦片,我们会随机选择起点。 否则,我们选择remaining列表中的第一个条目 - 这将是邻居最多的条目。 - 我们从所选索引处的
remaining list获取chunk_idx,并从列表中删除该块。 - 现在我们计算
chunk_x和chunk_y以告诉我们它在新地图上的位置。 - 我们将可变变量
neighbors设置为 0; 我们将再次计算邻居。 - 我们创建一个名为
Options的可变变量。 它的类型相当奇怪Vec<Vec<usize>>- 它是 vector 的 vector,每个 vector 都包含一个数组索引 (usize)。 我们将在此处存储每个方向的兼容选项 - 因此我们需要用于方向的外部 vector 和用于选项的内部 vector。 这些索引constraintsvector。 - 如果它不是地图上最左侧的块,则它可能在西侧有一个块 - 因此我们计算该块的索引。 如果西侧存在块(不是
None),那么我们将它的东向compatible_with列表添加到我们的Optionsvector 中。 我们递增neighbors以指示我们找到了一个邻居。 - 我们对东侧重复操作 - 如果它不是地图上最右侧的块。 我们递增
neighbors以指示我们找到了一个邻居。 - 我们对南侧重复操作 - 如果它不是地图上最底部的块。 我们递增
neighbors以指示我们找到了一个邻居。 - 我们对北侧重复操作 - 如果它不是地图上最顶部的块。 我们递增
neighbors以指示我们找到了一个邻居。 - 如果没有邻居,我们:
- 从
constraints中找到一个随机瓦片。 - 计算出我们将瓦片放置在
left_x、right_x、top_y和bottom_y中的边界。 - 将选定的瓦片复制到地图。
- 从
- 如果有邻居,我们:
- 将每个方向的所有选项插入到
HashSet中。 我们之前使用HashSet来去重我们的瓦片,这就是我们在这里所做的事情:我们删除了所有重复的选项,因此我们不会重复评估它们。 - 我们创建一个名为
possible_options的新 vector。 对于HashSet中的每个选项:- 将一个名为
possible的可变变量设置为true。 - 检查每个方向的
options,如果它与其邻居的偏好兼容 - 将其添加到possible_options。
- 将一个名为
- 如果
possible_options为空 - 那么我们就碰壁了,无法添加更多瓦片。 我们在父结构中将possible设置为 false 并退出! - 否则,我们从
possible_options中选择一个随机条目并将其绘制到地图上。
- 将每个方向的所有选项插入到
因此,虽然它是一个长函数,但它并不是一个真正复杂的函数。 它在每次迭代中查找可能的组合,并尝试应用它们 - 如果找不到则放弃并返回失败。
调用者已经在拍摄每次迭代的快照,因此如果我们使用我们的 wfc-test1.xp 文件 cargo run 项目,我们会得到如下结果:
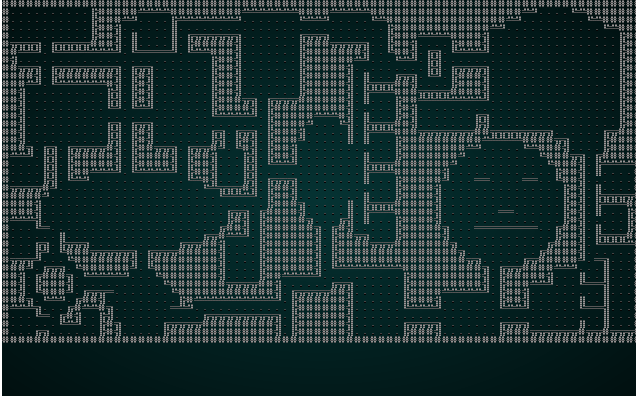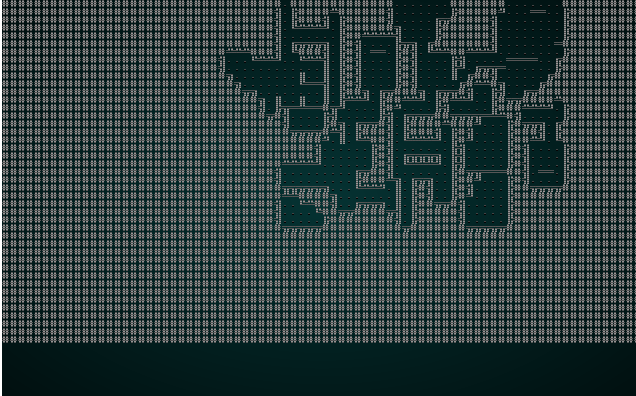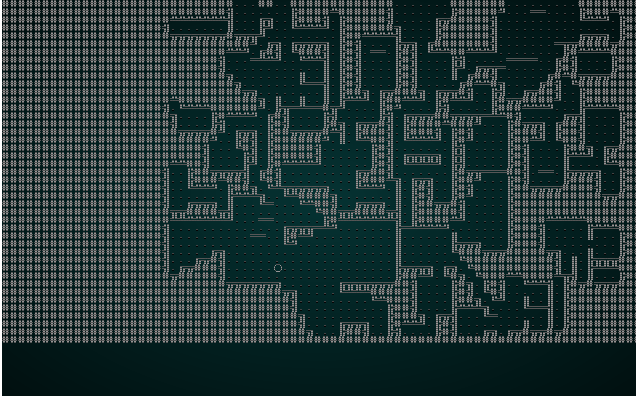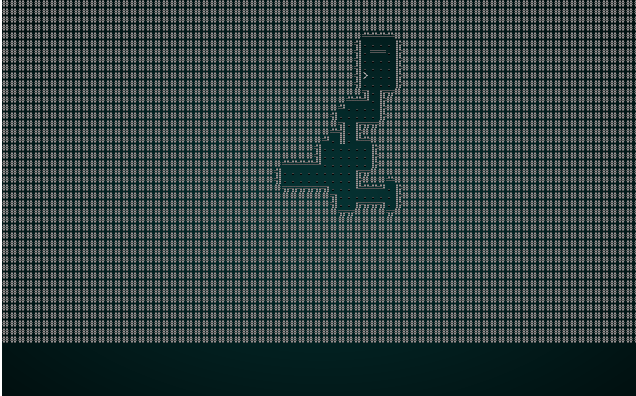 。
。
不是最好的地图,但你可以观看求解器缓慢地运行 - 一次放置一个瓦片。 现在让我们使用 wfc-test2.xmp 尝试一下,这是一组专为平铺设计的瓦片:
 。
。
这有点有趣 - 它像拼图一样布局,最终得到一张地图! 该地图的连接性不如人们希望的那样好,没有出口的边缘导致更小的游戏区域(在最后被剔除)。 这仍然是一个好的开始!
减小块大小
在这种情况下,我们可以通过将我们的 CHUNK_SIZE 常量减小到 3 来显着改善生成的地图。 使用测试地图 1 运行它会产生如下结果:
 。
。
这是一张更有趣的地图! 您也可以使用 wfc-test2.xp 尝试一下:
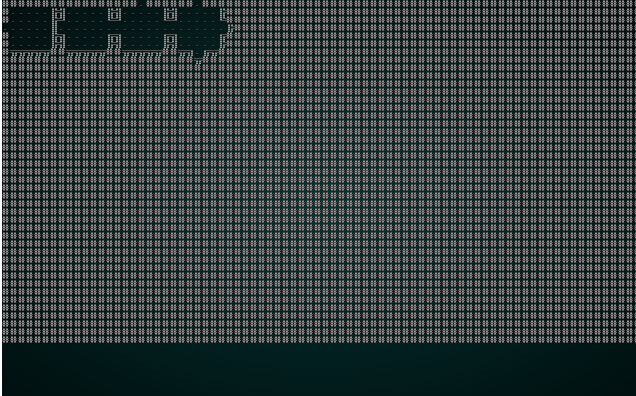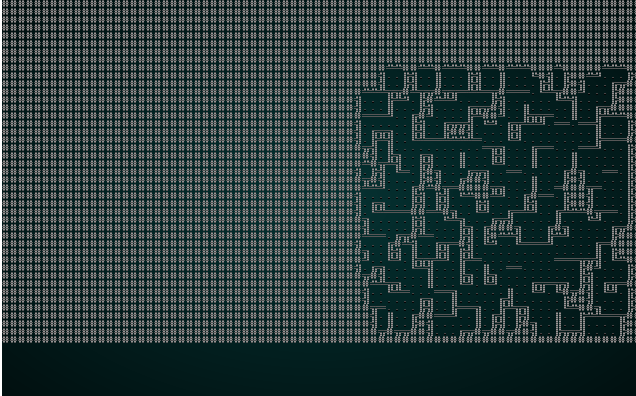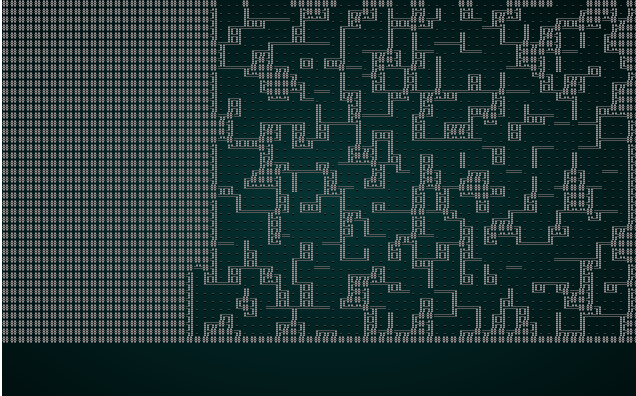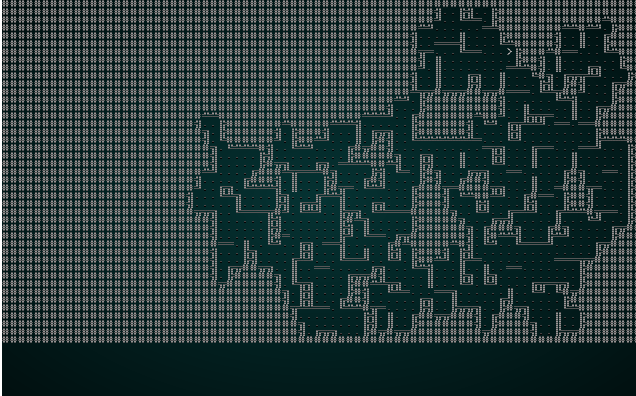 。
。
再一次,这是一张有趣且可玩的地图! 问题是我们有如此小的块大小,以至于邻接关系真的没有那么多有趣的选项 - 3x3 网格真的限制了您可以在地图上拥有的可变性! 因此,我们将使用 5 的块大小尝试 wfc-test1.xp:
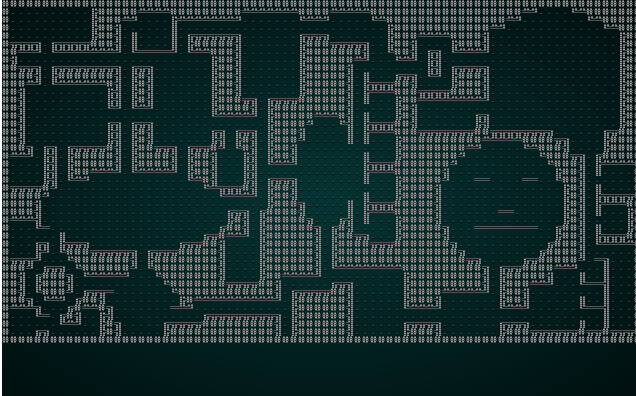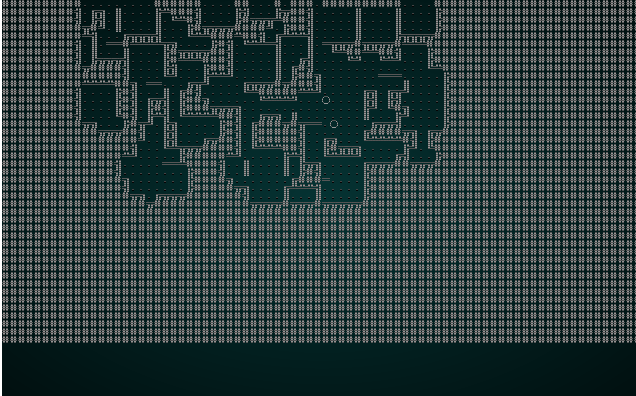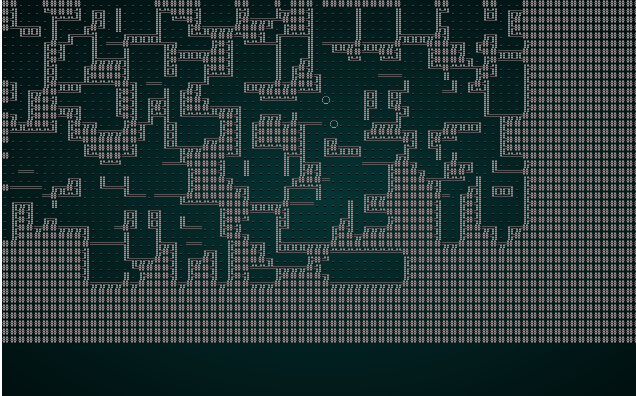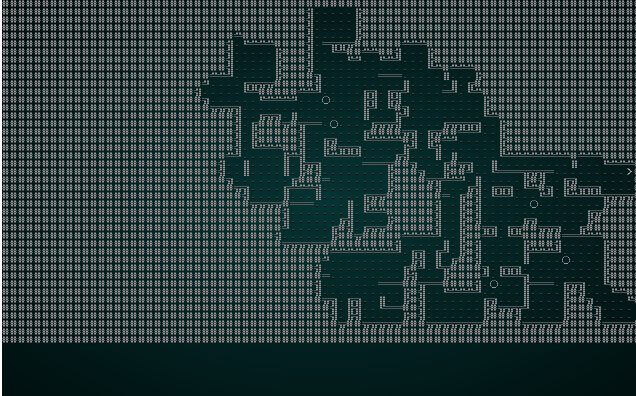 。
。
更像样了! 它与我们可能尝试以另一种方式生成的地图没有太大的不同。
利用读取其他地图类型的能力
与其加载我们的 .xp 文件之一,不如输入 CellularAutomata 运行的结果,并使用它作为具有大 (8) 块的种子。 使用我们拥有的结构,这非常容易! 在我们的 build 函数中:
#![allow(unused)] fn main() { const CHUNK_SIZE :i32 = 8; let mut ca = super::CellularAutomataBuilder::new(0); ca.build_map(); self.map = ca.get_map(); for t in self.map.tiles.iter_mut() { if *t == TileType::DownStairs { *t = TileType::Floor; } } }
请注意,我们正在删除下楼梯 - 细胞自动机生成器将放置一个,我们不希望到处都是楼梯! 这给出了非常令人愉悦的结果:
 。
。
改进邻接关系 - 并增加拒绝的风险!
我们已经拥有的已经是一个非常可行的解决方案 - 您可以使用它制作出色的地图,尤其是在您使用其他生成器作为种子时。 在曲折的拼图地图上,它没有生成我们想要的邻接关系。 通过使匹配器更具体,存在一些失败的小风险,但无论如何让我们尝试一下。 在我们构建兼容性矩阵的代码中,找到注释 `这
