Voronoi 蜂巢/单元格地图

关于本教程

本教程是免费和开源的，所有代码都使用 MIT 许可证 - 因此您可以随意使用。我希望您会喜欢本教程，并制作出色的游戏！

如果您喜欢这个教程并希望我继续写作，请考虑支持我的 Patreon。

我们之前在生成点放置中接触过 Voronoi 图。在本节中，我们将使用它们来制作地图。该算法基本上将地图细分为多个区域，并在它们之间放置墙壁。结果有点像蜂巢。您可以调整距离/邻接算法来调整结果。

脚手架

我们将像之前的章节一样制作脚手架，在 voronoi.rs 中创建 VoronoiBuilder 结构。我们还将调整 random_builder 函数，使其目前只返回 VoronoiBuilder。

构建 Voronoi 图

在之前的用法中，我们略过了如何实际制作 Voronoi 图 - 并依赖于 rltk 库中的 FastNoise 库。这当然很好，但它并没有真正向我们展示它是如何工作的 - 并且提供了非常有限的调整机会。所以 - 我们将自己制作一个。

制作 Voronoi 噪声的第一步是填充一组“种子”。这些是在地图上随机选择（但不是重复）的点。我们将使种子的数量成为一个变量，以便稍后可以对其进行调整。这是代码：

#![allow(unused)]
fn main() {
let n_seeds = 64;
let mut voronoi_seeds : Vec<(usize, rltk::Point)> = Vec::new();

while voronoi_seeds.len() < n_seeds {
    let vx = rng.roll_dice(1, self.map.width-1);
    let vy = rng.roll_dice(1, self.map.height-1);
    let vidx = self.map.xy_idx(vx, vy);
    let candidate = (vidx, rltk::Point::new(vx, vy));
    if !voronoi_seeds.contains(&candidate) {
        voronoi_seeds.push(candidate);
    }
}
}

这创建了一个 vector，每个条目包含一个 tuple。在该 tuple 中，我们存储了地图位置的索引，以及包含 x 和 y 坐标的 Point （如果我们愿意，可以跳过保存这些并从索引计算，但我认为这样更清晰）。然后我们随机确定一个位置，检查以确保我们尚未滚动到该位置，并将其添加。我们重复此过程，直到获得所需数量的种子。64 相当多，但会产生相对密集的蜂巢状结构。

下一步是确定每个单元格的 Voronoi 成员资格：

#![allow(unused)]
fn main() {
let mut voronoi_distance = vec![(0, 0.0f32) ; n_seeds];
let mut voronoi_membership : Vec<i32> = vec![0 ; self.map.width as usize * self.map.height as usize];
for (i, vid) in voronoi_membership.iter_mut().enumerate() {
    let x = i as i32 % self.map.width;
    let y = i as i32 / self.map.width;

    for (seed, pos) in voronoi_seeds.iter().enumerate() {
        let distance = rltk::DistanceAlg::PythagorasSquared.distance2d(
            rltk::Point::new(x, y),
            pos.1
        );
        voronoi_distance[seed] = (seed, distance);
    }

    voronoi_distance.sort_by(|a,b| a.1.partial_cmp(&b.1).unwrap());

    *vid = voronoi_distance[0].0 as i32;
}
}

在这段代码块中，我们：

创建一个新的 vector，名为 voronoi_distance。它包含 usize 和 f32 (浮点数) 的元组，并预先创建了 n_seeds 个条目。我们可以为每次迭代都创建它，但是重用同一个会快得多。我们将其创建为零。
我们创建一个新的 voronoi_membership 向量，其中包含地图上每个瓦片的一个条目。我们将它们全部设置为 0。我们将使用它来存储瓦片属于哪个 Voronoi 单元格。
对于 voronoi_membership 中的每个瓦片，我们获得一个枚举器（索引号）和值。我们可变地拥有它，因此我们可以进行更改。
1. 我们从枚举器 (i) 计算瓦片的 x 和 y 位置。
2. 对于 voronoi_seeds 结构中的每个条目，我们获得索引（通过 enumerate()）和位置元组。
  1. 我们使用 PythagorasSquared 算法计算从种子到当前瓦片的距离。
  2. 我们将 voronoi_distance[seed] 设置为种子索引和距离。
3. 我们按距离对 voronoi_distance 向量进行排序，因此最近的种子将是第一个条目。
4. 我们将瓦片的 vid (Voronoi ID) 设置为 voronoi_distance 列表中的第一个条目。

您可以用更简单的英语总结一下：每个瓦片都被赋予了 Voronoi 组的成员资格，该组的种子在物理上离它最近。

接下来，我们使用它来绘制地图：

#![allow(unused)]
fn main() {
for y in 1..self.map.height-1 {
    for x in 1..self.map.width-1 {
        let mut neighbors = 0;
        let my_idx = self.map.xy_idx(x, y);
        let my_seed = voronoi_membership[my_idx];
        if voronoi_membership[self.map.xy_idx(x-1, y)] != my_seed { neighbors += 1; }
        if voronoi_membership[self.map.xy_idx(x+1, y)] != my_seed { neighbors += 1; }
        if voronoi_membership[self.map.xy_idx(x, y-1)] != my_seed { neighbors += 1; }
        if voronoi_membership[self.map.xy_idx(x, y+1)] != my_seed { neighbors += 1; }

        if neighbors < 2 {
            self.map.tiles[my_idx] = TileType::Floor;
        }
    }
    self.take_snapshot();
}
}

在这段代码中，我们访问除了最外边缘之外的每个瓦片。我们计算有多少相邻的瓦片属于 不同的 Voronoi 组。如果答案是 0，则它完全在该组中：因此我们可以放置地板。如果答案是 1，则它仅与 1 个其他组接壤 - 因此我们也可以放置地板（以确保我们可以在地图上行走）。否则，我们将瓦片保留为墙壁。

然后，我们运行与之前使用过的相同的剔除和放置代码。如果您现在 cargo run 该项目，您将看到一个令人愉悦的结构：

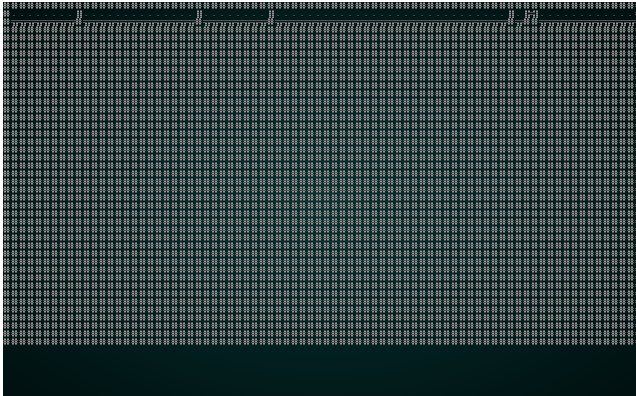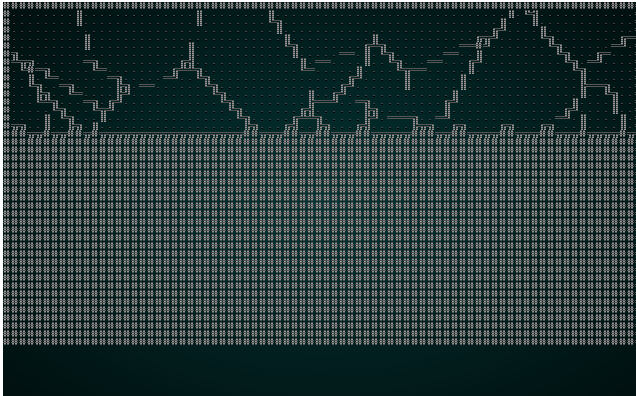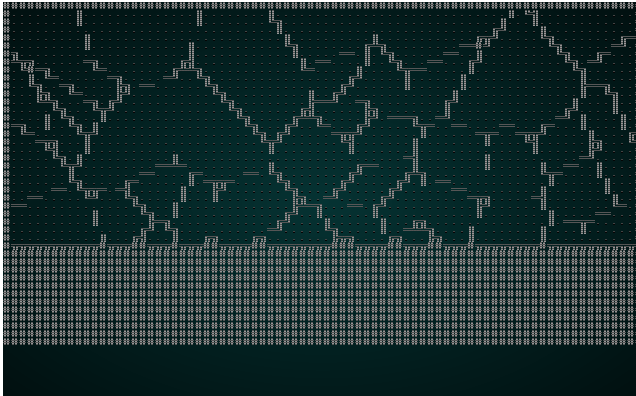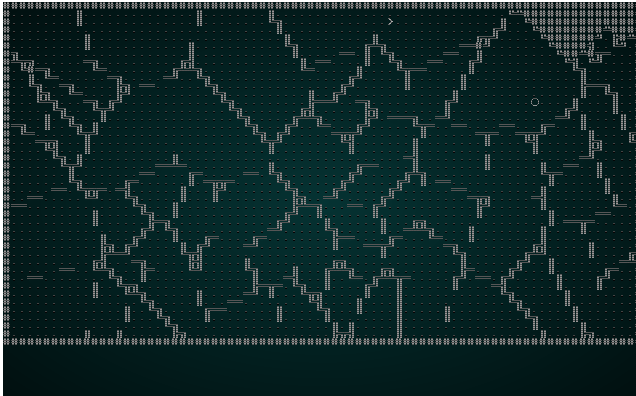Screenshot .

调整蜂巢

有两个明显的变量可以暴露给构建器：种子的数量，以及要使用的距离算法。我们将更新结构签名以包含这些：

#![allow(unused)]
fn main() {
#[derive(PartialEq, Copy, Clone)]
pub enum DistanceAlgorithm { Pythagoras, Manhattan, Chebyshev }

pub struct VoronoiCellBuilder {
    map : Map,
    starting_position : Position,
    depth: i32,
    history: Vec<Map>,
    noise_areas : HashMap<i32, Vec<usize>>,
    n_seeds: usize,
    distance_algorithm: DistanceAlgorithm
}
}

然后我们将更新 Voronoi 代码以使用它们：

#![allow(unused)]
fn main() {
fn build(&mut self) {
    let mut rng = RandomNumberGenerator::new();

    // Make a Voronoi diagram. We'll do this the hard way to learn about the technique!
    // 制作 Voronoi 图。我们将用比较复杂的方式来做，以了解这项技术！
    let mut voronoi_seeds : Vec<(usize, rltk::Point)> = Vec::new();

    while voronoi_seeds.len() < self.n_seeds {
        let vx = rng.roll_dice(1, self.map.width-1);
        let vy = rng.roll_dice(1, self.map.height-1);
        let vidx = self.map.xy_idx(vx, vy);
        let candidate = (vidx, rltk::Point::new(vx, vy));
        if !voronoi_seeds.contains(&candidate) {
            voronoi_seeds.push(candidate);
        }
    }

    let mut voronoi_distance = vec![(0, 0.0f32) ; self.n_seeds];
    let mut voronoi_membership : Vec<i32> = vec![0 ; self.map.width as usize * self.map.height as usize];
    for (i, vid) in voronoi_membership.iter_mut().enumerate() {
        let x = i as i32 % self.map.width;
        let y = i as i32 / self.map.width;

        for (seed, pos) in voronoi_seeds.iter().enumerate() {
            let distance;
            match self.distance_algorithm {
                DistanceAlgorithm::Pythagoras => {
                    distance = rltk::DistanceAlg::PythagorasSquared.distance2d(
                        rltk::Point::new(x, y),
                        pos.1
                    );
                }
                DistanceAlgorithm::Manhattan => {
                    distance = rltk::DistanceAlg::Manhattan.distance2d(
                        rltk::Point::new(x, y),
                        pos.1
                    );
                }
                DistanceAlgorithm::Chebyshev => {
                    distance = rltk::DistanceAlg::Chebyshev.distance2d(
                        rltk::Point::new(x, y),
                        pos.1
                    );
                }
            }
            voronoi_distance[seed] = (seed, distance);
        }

        voronoi_distance.sort_by(|a,b| a.1.partial_cmp(&b.1).unwrap());

        *vid = voronoi_distance[0].0 as i32;
    }

    for y in 1..self.map.height-1 {
        for x in 1..self.map.width-1 {
            let mut neighbors = 0;
            let my_idx = self.map.xy_idx(x, y);
            let my_seed = voronoi_membership[my_idx];
            if voronoi_membership[self.map.xy_idx(x-1, y)] != my_seed { neighbors += 1; }
            if voronoi_membership[self.map.xy_idx(x+1, y)] != my_seed { neighbors += 1; }
            if voronoi_membership[self.map.xy_idx(x, y-1)] != my_seed { neighbors += 1; }
            if voronoi_membership[self.map.xy_idx(x, y+1)] != my_seed { neighbors += 1; }

            if neighbors < 2 {
                self.map.tiles[my_idx] = TileType::Floor;
            }
        }
        self.take_snapshot();
    }
    ...
}

作为一个测试，让我们更改构造函数以使用 Manhattan 距离。结果将如下所示：

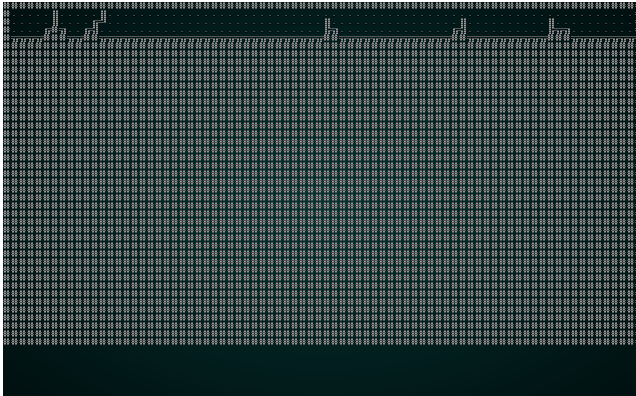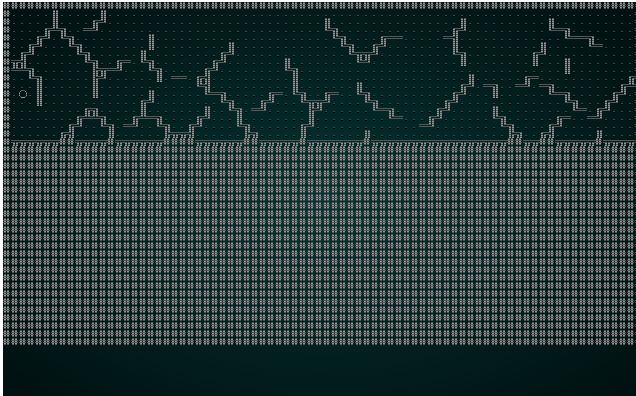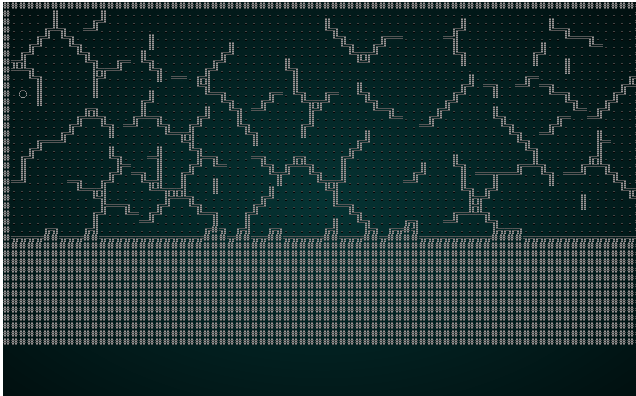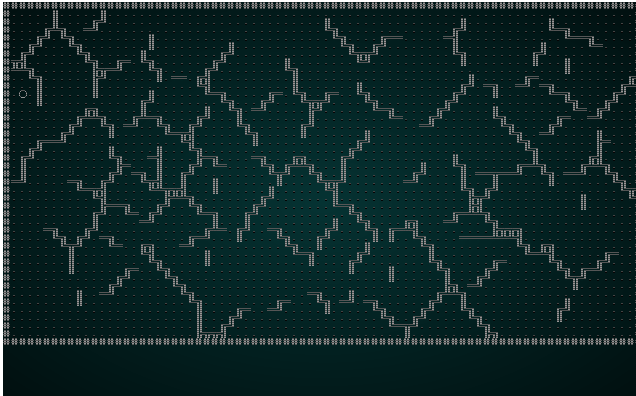Screenshot .

请注意线条是如何更直，更少有机感的。这就是 Manhattan 距离的作用：它像曼哈顿出租车司机一样计算距离 - 行数加列数，而不是直线距离。

恢复随机性

因此，我们将为每种噪声类型放入几个构造函数：

#![allow(unused)]
fn main() {
pub fn pythagoras(new_depth : i32) -> VoronoiCellBuilder {
    VoronoiCellBuilder{
        map : Map::new(new_depth),
        starting_position : Position{ x: 0, y : 0 },
        depth : new_depth,
        history: Vec<Map>,
        noise_areas : HashMap::new(),
        n_seeds: 64,
        distance_algorithm: DistanceAlgorithm::Pythagoras
    }
}

pub fn manhattan(new_depth : i32) -> VoronoiCellBuilder {
    VoronoiCellBuilder{
        map : Map::new(new_depth),
        starting_position : Position{ x: 0, y : 0 },
        depth : new_depth,
        history: Vec<Map>,
        noise_areas : HashMap::new(),
        n_seeds: 64,
        distance_algorithm: DistanceAlgorithm::Manhattan
    }
}
}

然后我们将恢复 random_builder，使其再次随机：

#![allow(unused)]
fn main() {
pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> {
    let mut rng = rltk::RandomNumberGenerator::new();
    let builder = rng.roll_dice(1, 16);
    match builder {
        1 => Box::new(BspDungeonBuilder::new(new_depth)),
        2 => Box::new(BspInteriorBuilder::new(new_depth)),
        3 => Box::new(CellularAutomataBuilder::new(new_depth)),
        4 => Box::new(DrunkardsWalkBuilder::open_area(new_depth)),
        5 => Box::new(DrunkardsWalkBuilder::open_halls(new_depth)),
        6 => Box::new(DrunkardsWalkBuilder::winding_passages(new_depth)),
        7 => Box::new(DrunkardsWalkBuilder::fat_passages(new_depth)),
        8 => Box::new(DrunkardsWalkBuilder::fearful_symmetry(new_depth)),
        9 => Box::new(MazeBuilder::new(new_depth)),
        10 => Box::new(DLABuilder::walk_inwards(new_depth)),
        11 => Box::new(DLABuilder::walk_outwards(new_depth)),
        12 => Box::new(DLABuilder::central_attractor(new_depth)),
        13 => Box::new(DLABuilder::insectoid(new_depth)),
        14 => Box::new(VoronoiCellBuilder::pythagoras(new_depth)),
        15 => Box::new(VoronoiCellBuilder::manhattan(new_depth)),
        _ => Box::new(SimpleMapBuilder::new(new_depth))
    }
}
}

总结

这又是我们掌握的一种算法！我们现在真的有足够的能力编写一个相当不错的 roguelike 游戏了，但还有更多内容！

本章的源代码可以在这里找到

使用 Rust 开发肉鸽游戏教程

Voronoi 蜂巢/单元格地图

脚手架

构建 Voronoi 图

调整蜂巢

恢复随机性

总结

在您的浏览器中使用 web assembly 运行本章的示例（需要 WebGL2）